• Онлайн: 2
Содержание
Арифметические ребусы
По названию можно подумать, что арифметические ребусы - это обычные ребусы, в которых при кодировании слова используются цифры и числа. Например, «100 Л» – это «стол», «7Я» – «семья» и т.п. Но это не так. То, что я привёл в примере – это обычные ребусы. А вот арифметические ребусы к обычным ребусам вообще не имеют никакого отношения, но исторически сложилось, что подобные задачки называют именно так.
Арифметическими ребусами называют обычные выражения и примеры, в которых все или большая часть цифр заменена какими-либо символами или буквами. В буквенном арифметическом ребусе каждая буква означает одну определённую цифру. В символьных ребусах со звёздочками, кружочками и точками каждый значок может обозначать любую цифру от 0 до 9. Причём цифры могут повторяться, какие-то могут вообще не использоваться. Единственное исключение – числа не начинаются на 0. Иногда вместо всего числа ставят знак «?», то есть даже сколько цифр в числе не известно. Решить такой ребус – это значит восстановить первоначальную запись примера.
При решении задач такого типа требуется внимательность к очевидным арифметическим действиям, хорошее знание арифметики и умение логически рассуждать. Арифметика - это не только 2+2=4. Это также глубокое понимание принципов порядкового исчисления, знание правил раскрытия скобок, признаков делимости, разложения на множители, правил действия с дробями и степенями, пропорциями, что такое натуральные, простые и составные числа, как найти НОК и НОД, как посчитать сумму последовательности и многое другое. При решении арифметических ребусов могут понадобиться и некоторые знания алгебры, например, решение уравнений и систем уравнений.
Некоторые математические задачи могут оказаться слишком сложными для использования в обычных (не математических) квестах, поэтому выбирать их следует внимательно.
Арифметических ребусов, как и обычных ребусов, – бесконечное множество. Но все их можно поделить на несколько видов.
Пустышки
В таких арифметических ребусах все цифры заменены на точки, звёздочки, кружочки, в общем, на одинаковые символы.
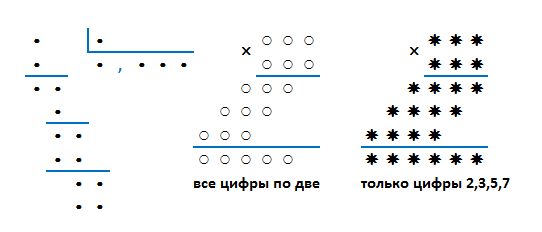
В обычных «пустышках» часто для подсказки открывают некоторые цифры, либо какую-то из цифр (какую точно, не известно) помечают специальным знаком. Получаются «пустышки с подсказками».
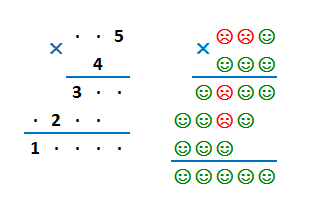
C картинками
Последнее время в интернете стали популярны ребусы, в которых задана система уравнений, где неизвестные заменены картинками. Например, вот такая задачка:

Она сводится к решению обычной системы из двух уравнений с двумя неизвестными.
Перенесём все неизвестные налево, известные направо, домножим второе уравнение на 2 и из первого уравнения вычтем второе. Получим 3x-2x + 2y-2y = 1-(-4). Сокращаем и получаем x=5, а значит y=7. Простейшая задачка для ученика 4-5 класса.
Начиналось-то всё просто, но потом картинки стали с подвохом. Например, вот эта. С виду ничего необычного.

Видим авокадо (x), связку бананов (y), апельсины (z).
Из первого уравнения x=10, подставляем x во второе, получаем y=4, подставляем y в третье, получаем z=1, значит 1+10+4=15. Всё вроде бы просто. Так будут решать 95% людей. Но 5% заметят, что нижняя связка бананов поменьше, чем верхние. Верхние связки бананов = 4, потому что там по 4 банана. А вот в нижней 3 банана, значит её нужно считать как 3. А теперь внимательно смотрим на апельсины. Сколько их внизу? Один? А не половинка ли? Похоже, что в третьей строке целый апельсин разрезан пополам. И получается совсем другая система.
И значит, что целый апельсин = 2, а пол-апельсина = 1. И значит, что правильным ответом будет 1+10+3 = 14, а не 15.
Считать апельсины целыми или половинками в общем-то не важно. Всё равно внизу будет единица. Главное, что бананов три, а не четыре. Замечу, что некоторые особо дотошные люди могут утверждать, что в третьем уравнении не две половинки, а половинка и целый, то есть полтора апельсина. Но тогда задача в целых числах не решается, а это некрасиво :) Поэтому мы так считать не будем.
Бывают и ещё более замороченные задачки с ещё более глубокими подвохами. Например, вот такая, от Леонида Каганова:
Попробуйте её решить сами без подсказок, а потом почитайте на сайте по ссылке, до чего дорешались там :)
Чёт и нечет
Чётные цифры (0,2,4,6,8) помечены буквой Ч, а нечётные (1,3,5,7,9) - буквой Н.
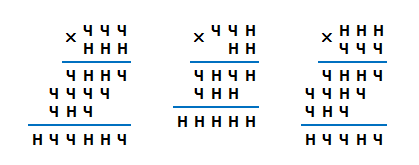
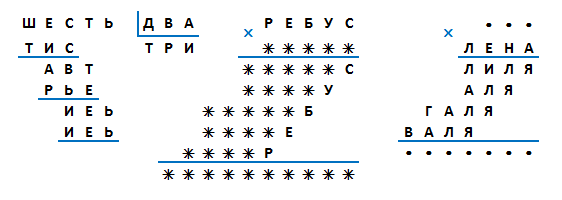
С буквами
Это классика математических ребусов, в них цифры заменены буквами. Чаще всего авторы подобных задач стараются так подобрать буквы, чтобы в отдельных местах читались слова. Остальные же места, где слова не получаются, остаются, как в пустышках. Иногда в некоторых местах также оставляют подсказки.
Рамки
У нас есть 10 цифр, а в русском языке довольно много слов, состоящих из 10-ти разных неповторяющихся букв. Их можно использовать как ключевые слова в головоломках, которые некоторые называют «ребусы с ключевыми словами», а я называю «Рамки».
Каждая такая задачка состоит из 6-ти уравнений, связанных между собой знаками « + », « – », « × », « : », « = ». Цифры зашифрованы буквами, разным цифрам соответствуют разные буквы. Обычно используется 10 букв для 10-ти цифр, но можно составить пример и из меньшего количества цифр, тогда и букв будет меньше.
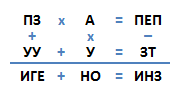
Это настоящая математическая задача, причём довольно сложная, поэтому подойдёт не для каждого квеста. Решается задача так.
Рассмотрим первый столбец ПЗ+УУ=ИГЕ. Сумма двух двузначных чисел не может быть больше 99+99=198, значит, И=1.
В равенстве ПЕП-ЗТ=ИНЗ (третий столбец) видно, что к трёхзначному числу ИНЗ, начинающемуся на 1, прибавили двузначное число ЗТ и получили снова трёхзначное ПЕП. П - не 1, так как 1 уже занято буквой И. Выходит, П=2, потому что больше оно быть не может (потому что 298 - максимально возможная сумма двухзначного и трёхзначного, начинающегося на 1).
В третьей строке ИГЕ+НО=ИНЗ при сложении Г десятков с Н десятками снова получается Н десятков. Это может быть только если Г=0 или Г=9. Но если бы Г было равно 9, то был бы перенос единицы в разряд сотен, а у нас было И и осталось И. Значит, Г=0.
Итак, Г=0, И=1, П=2. А поэтому в равенстве ПЗ+УУ=ИГЕ У может быть или 7, или 8, ведь нам надо к двум с чем-то десяткам прибавить двузначное число, и чтобы получилось больше сотни. Пусть, У=8. Тогда из УУ+У=ЗТ следует, что Т=6 и З=9. Но тогда в разности ПЕП-ЗТ=ИНЗ получаем П=5. Но ведь П=2! Значит, У≠8. Следовательно, У=7. Тогда из УУ+У=ЗТ получаем Т=4, З=9. Равенство ПЗ+УУ=ИГЕ при З=8 и У=7 даёт нам ещё одну букву: Е=5.
В сумме ИГЕ+НО=ИНЗ Е=5, З=8, а значит, О=3. В третьем столбце нам уже стали известны все буквы, кроме Н. Поэтому, значение её легко находится: Н=6. И, наконец, из равенства АxУ=НО получаем А=9.
В результате имеем: 0123456789=ГИПОТЕНУЗА. Слово разгадано, его можно как-то использовать дальше в виде ключевого слова или подсказки для решения следующих квестовых задач.
Ниже приведены примеры «математических ребусов».
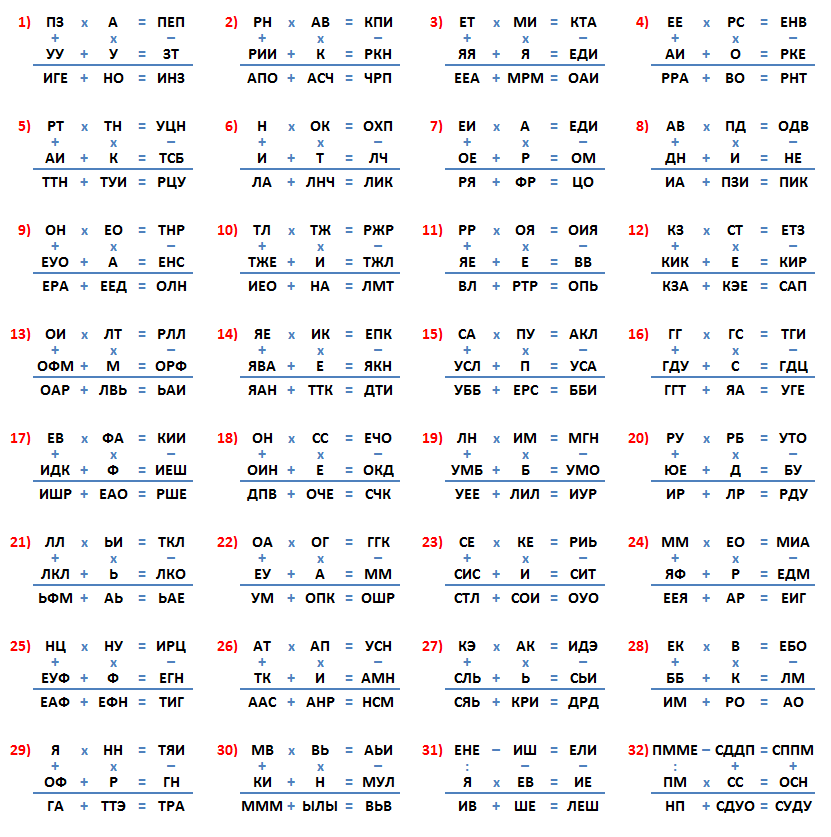
Ответы: 1-гипотенуза, 2-справочник, 3-демократия, 4-крестовина, 5-струбцина, 6-хлопчатник, 7-деформация, 8-заповедник, 9-лесотундра, 10-метилоранж, 11-проявитель, 12-экспертиза, 13-вольфрамит, 14-пятидневка, 15-республика, 16-дегустация, 17-дешифровка, 18-подсвечник, 19-глубиномер, 20-трудолюбие, 21-фильмотека, 22-погремушка, 23-ускоритель, 24-демография, 25-центрифуга, 26-манускрипт, 27-эскадрилья, 28-меблировка, 29-этнография, 30-умывальник, 31-Лев Яшин, 32-сподумен.
Кирпичики
Внешний вид задачек такого рода напоминает столбики, сложенные из кирпичей, поэтому назову их «кирпичики».
Правила такие:
- каждый квадратик - это одна цифра;
- ни одно число не начинается на 0;
- сумма чисел каждого вертикального ряда равна результату соответствующей горизонтальной строки;
- действия производятся последовательно слева направо, то есть правила приоритета не работают.
Решим для примера вот такие «кирпичики»:
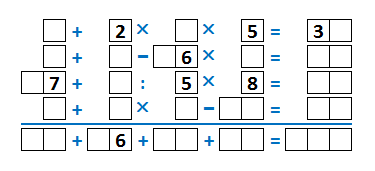
Для начала, используя правило [3], зеркально относительно диагонали отразим и дополним результаты столбцов и строк. Шестёрка из результата второго столбца скопируется во вторую строку, а тройка из результата первой строки скопируется в первый столбец.
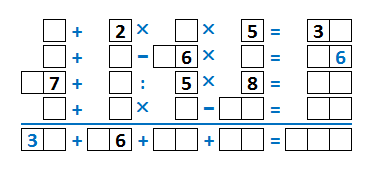
Посмотрим на вторую строку. Первые два числа однозначные, значит их сумма не больше 18, а значит отнять можно только 16, иначе у нас получится отрицательное число. Значит, третье число во второй строке 16. Допустим, сумма двух первых чисел 17. Тогда 17-16=1. Один умножить на однозначное число и получается двузначное - так не бывает. Значит, сумма двух первых чисел строки не 17, а 18. Значит, это обе девятки, 9+9-16=2. А на какое однозначное число надо умножить двойку, чтобы получилось двузначное с шестёркой на конце? На 8! Итого, получили целиком вторую строку: 9+9-16×8=16. Не забываем, что порядок действий - слева направо, то есть как будто запись вот такая: [(9+9)-16]×8=16.
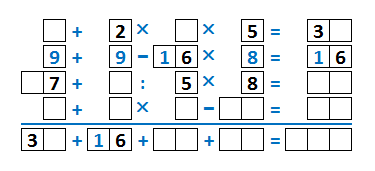
Теперь смотрим на второй столбец. 16-2-9=5. То есть третье и четвёртое числа во втором столбце дают в сумме 5. Теперь посмотрим на третью строку. Результат сложения двузначного числа, оканчивающегося семёркой и второго числа должен делиться на 5, а значит должен заканчиваться на 5 или 0. А значит, третье число во втором столбце должно быть или 3 или 8. Но оно ведь должно быть меньше пяти! Значит, это тройка. А тогда четвёртое число во втором столбце - это двойка.
Результат первой строки - это 30 или 35, так как в конце стоит умножение на 5. Значит, сумма первого столбца тоже 30 или 35.
В первом столбце третье число - это 17, или 27, или 37, или т.д. Допустим, 27. Тогда 27+9=36, а это уже больше, чем весь возможный результат столбца - 35. Значит, у нас не 27, а 17. Итого, получилась третья строка: 17+3:5×8=32.
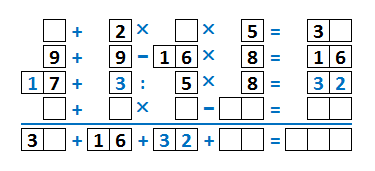
Итак, результат первой строки 30 или 35. Пусть 35. Тогда сумма первых двух чисел равна 7, а третье число - единица. Значит, третий столбец начинается с единицы. Получается, что четвёртое число в третьем столбце должно равняться 32-1-16-5=10. Но оно однозначное! Мы допустили, что результат первой строки 35 и пришли к противоречию. Значит, не 35, а 30.
А раз 30, думаем над первой строкой. Третье число, как мы уже установили, не единица. Значит, двойка. Любого другого будет уже много. Получаем первую строку: 1+2x2x5=30. Ну и тут уже легко получается четвёртая строка: 3+2×9-12=33. И вот он результат:
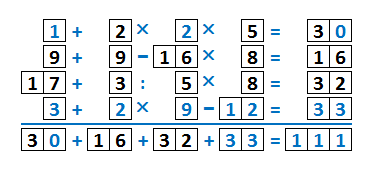
Как вы заметили, самое нижнее правое число (сумма последней строки, она же сумма последнего столбца) получилось в самом конце решения головоломки. Его невозможно получить в результате промежуточных вычислений, а значит, что такие типы задач можно применять, если в квесте нужно загадать какое-то трёхзначное число. Например, шифр от сейфа. Хотя не, 1000 комбинаций и перебрать можно. Допустим, надо ввести код для отключения бомбы и ошибаться нельзя. Вот тогда три цифры - самый раз ![]() .
.
Ниже набор из 24 готовых «кирпичиков» с ответами:
Замочки

Этот тип задач похож на зашифрованные определённым кодом «кирпичики». Выглядит код так, как будто цифры прикрыли квадратиками, но выступающие части цифр остались видны. Символы, которыми зашифрованы цифры, похожи на амбарные замки, поэтому их так и называют, «замочки» (иногда их называют «коврики», потому что в целом задачка похожа на квадратный вышитый половичок).
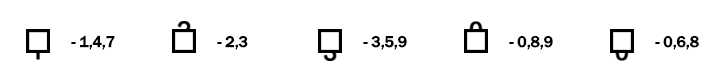
Если бы у каждой цифры был свой значок, то это был бы полноценный шифр замены, но здесь один символ соответствует разным цифрам. И понять, какая цифра где скрылась, помогут знания математики. Знаки показывают действия, которые производятся с числами по горизонтали и по вертикали. Последовательность действий такая же, как и в «кирпичиках» - слева-направо и сверху-вниз без учёта приоритета. И решаются «замочки», соответственно, так же, как и «кирпичики». А применять их в квестах можно, например, для открывания «цифровых замочков» на закрытых дверях. Отгадывающим надо будет либо решить такой ребус и узнать правильные 4 цифры, либо по порядку перебирать 10000 возможных вариантов комбинаций 4 цифр, пока не попадётся подходящий. Для механических замков такой метод перебора подойдёт, а вот электронные замки могут иметь защиту на количество неправильных попыток, поэтому лучше, конечно, решать, а не подбирать.

Разберём пример:
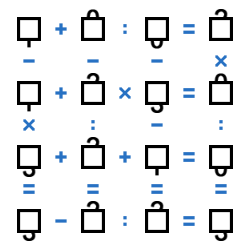
Во второй строке сумма первых двух цифр заведомо больше двух. Третья цифра - это 3, 5 или 9. Результат - однозначное число, значит третья цифра строки 3, а тогда в результате может быть только 9. И значит, первые две цифры - 1 и 2. Получили вторую строку: (1+2)x3=9.
Теперь посмотрим на первый столбец. Первая цифра не равна второй, иначе в результате получился бы ноль. Возможны варианты: 4-1 и 7-1, и оба они больше 2, а третья цифра - 3,5 или 9. Значит, первая цифра - 4, третья - 3, а в результате 9. Получаем (4-1)x3=9.
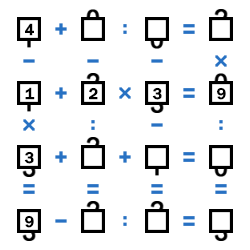
В третьей строке третья цифра не может быть равна 7, иначе в результате получилось бы двузначное число. Не может она быть и 4, так как при второй цифре 2 или 3 в результате было бы 9 или 10, а это не подходит. Значит, третья цифра третьей строки - это 1. Тогда вторая цифра - это 2, а результат - 6, т.е. 3+2+1=6.
Третий столбец отличается от третьей строки только взаимным расположением цифр, поэтому для третьего столбца получаем 6-3-1=2.
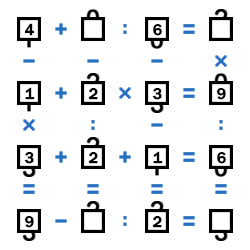
Смотрим на первую строку. В результате 2 или 3, а значит делится на 6 число 12 или 18. 18-4=14 не подходит, значит вторая цифра первой строки - это 8. Получаем первую строку (4+8):6=2.
Осталось посчитать результаты второго и четвёртого столбцов - 3 и 3. Всё, задача решена.
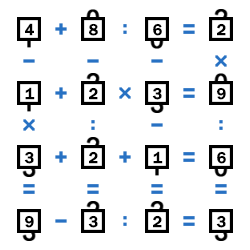
Ниже приведены примеры «замочков» и результаты их решения.
Чтобы не сильно мучиться в отрисовке этих картинок, пришлось немного покодить на яваскрипте (посмотрите исходный код страницы): http://nzdr.ru/coll/carpets.html.













