• Онлайн: 2
Содержание
Последовательности и перечисления
Числовые
Числовые последовательности — это один из основных объектов, рассмотрением которого занимается раздел математики под названием математический анализ. Его начинают изучать в старших классах средней школы и продолжают более подробно в институтах.
Числовых последовательностей бесчисленное число ![]() Но с точки зрения создания головоломок и занимательных задач нам интересно работать с простыми, известными и интересными последовательностями. Задачка может при этом выглядеть очень просто: «Продолжи последовательность чисел…»
Но с точки зрения создания головоломок и занимательных задач нам интересно работать с простыми, известными и интересными последовательностями. Задачка может при этом выглядеть очень просто: «Продолжи последовательность чисел…»
- Натуральные числа — 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 … (ими можно посчитать, например, яблоки)
- Чётные числа — 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 … (делятся без остатка на 2)
- Нечётные числа — 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 … (не делятся без остатка на 2)
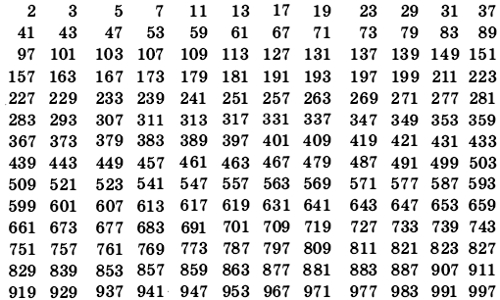
- Простые числа — 2 3 5 7 11 13 17 19 23 29 31 … (делятся только на себя и на 1)
- Числа Фибоначчи — 1 1 2 3 5 8 13 21 34 55 89 144 … (каждое последующее число равно сумме двух предыдущих чисел)
- Ряды Фарея — возрастающий ряд всех положительных несократимых правильных дробей, знаменатель которых меньше или равен n
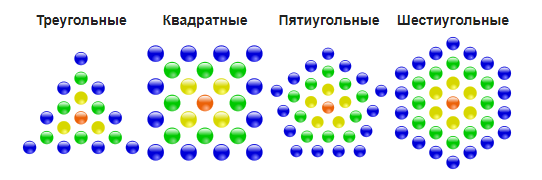
- Фигурные числа — если из камушков выкладывать разные фигуры – треугольники, квадраты, пятиугольники и т.п. – всё большего размера, то получатся последовательности фигурных чисел, соответственно, треугольных, квадратных, пятиугольных и т.д.
Причём фигурные числа могут быть как плоские, так и объёмные. Например, вот так как получаются квадратные пирамидальные числа.
А вот так образуются тетраэдральные числа.
Также последовательности чисел можно получить, подсчитывая число вершин, рёбер и граней в различных объёмных фигурах типа платоновых тел, архимедовых тел, многогранников Джонсона и т.п.
А ещё можно подсчитывать число всевозможных полимино.
Эти последовательности можно придумывать и продолжать бесконечно. Чтобы собрать в одном месте и классифицировать все такие последовательности был создан проект The On-Line Encyclopedia of Integer Sequences® или OEIS® (Онлайн-энциклопедия целочисленных последовательностей). На их сайте можно найти практически любую из известных целочисленных последовательностей.
Нематематические
Бывают такие числовые последовательности, которые не очень относятся к математике. Например, порядок чисел на барабане в казино или на дартсе.
Системы счисления
Позиционные системы счисления на разной основе:
- Двоичная: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10000, 10001, …
- Троичная: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100, 101, 102, 110, 111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212, 220, 221, 222, 1000, …
- Восьмеричная: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, 20, 21, 22, 23, 24, 25, 26, 27, 30, 31, 32, …
- Десятичная: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, …
- Шестнадцатеричная: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, …
- 32-ричная: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, 10, 11, …
В разных странах в разные времена применялись различные, в том числе непозиционные системы счисления. Если сейчас записать этими числами даже обычный ряд натуральных чисел, то получится настоящая головоломка.
Вавилонская поместная нумерация
Древнегреческая нумерация
Римские цифры
Славянская нумерация
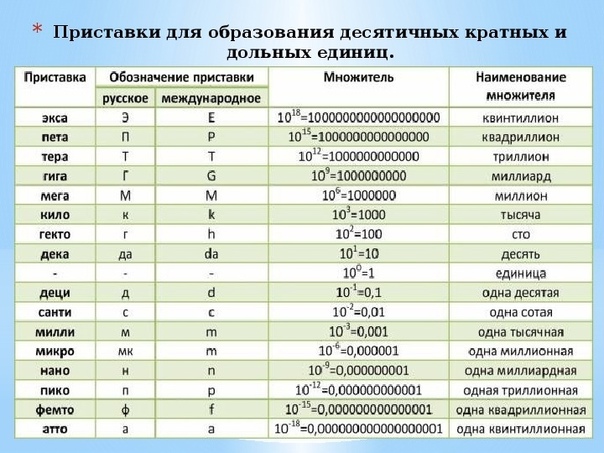
Названия кратных и дольных единиц
Нечисловые
А какие бывают нечисловые последовательности? Да любые! Конечно, в своей основе они тоже имеют какую-то числовую последовательность (например, порядковый номер в виде натурального числа или какую-то величину), но говоря о таких последовательностях мы уже не думаем о числах и математике. Нечисловая последовательность – это скорее некий логический ряд, перечень чего-либо, отсортированный по какому-нибудь общему для его элементов критерию. Например, список богатейших людей мира за 2024 год по данным журнала Forbes.
Кстати, иногда такие перечисления могут быть не очень фиксированными или постоянными. Например, список президентов какой-либо страны или чемпионов в какой-нибудь олимпийской дисциплине постоянно пополняется. Список стран, отсортированный по размеру ВПП каждый год меняется.
При этом последовательность может быть «ожидаемым списком», то есть некоторые пункты будут стоять на своём месте с определённой долей вероятности. Например, известный вопрос из «Что Где Когда»: «Внимательно прочитайте эти слова: любовь, дыхание, Рим, власть, колонна, чувство, небо. Назовите восьмое, дополнив логический ряд.» Объединяет эти слова то, что все они взяты из известных «числовых» фразеологизмов:
- первая любовь
- второе дыхание
- третий Рим
- четвёртая власть
- пятая колонна
- шестое чувство
- седьмое небо
- восьмое чудо света
- девятый вал
Соответственно, ответом на вопрос было «чудо» или «чудо света». Но этот список можно ведь легко изменить. Первой может быть не только «любовь», но и «леди», «ласточка» и даже «первый блин комом». А пятым пунктом может быть как и сам «пятый пункт» (графа «национальность» в некоторых документах СССР), но и «пятое колесо», «пятая точка» и т.д. Дело десятое, зарплата тринадцатая, а ещё бывают тридевятое царство и тридесятое государство.
Алфавиты
Самые известные нечисловые последовательности – это алфавиты:
- Русский — Аа Бб Вв Гг Дд Ее Ёё Жж Зз Ии Йй Кк Лл Мм Нн Оо Пп Рр Сс Тт Уу Фф Хх Цц Чч Шш Щщ Ъъ Ыы Ьь Ээ Юю Яя
- Латинский — Aa Bb Cc Dd Ee Ff Gg Hh Ii Jj Kk Ll Mm Nn Oo Pp Qq Rr Ss Tt Uu Vv Ww Xx Yy Zz
- Греческий — Αα Ββ Γγ Δδ Εε Ζζ Ηη Θθ Ιι Κκ Λλ Μμ Νν Ξξ Οο Ππ Ρρ Σσς Ττ Υυ Φφ Χχ Ψψ Ωω
- Глаголица — Ⰰⰰ Ⰱⰱ Ⰲⰲ Ⰳⰳ Ⰴⰴ Ⰵⰵ Ⰶⰶ Ⰷⰷ Ⰸⰸ Ⰹⰹ Ⰺⰺ Ⰻⰻ Ⰼⰼ Ⰽⰽ Ⰾⰾ Ⰿⰿ Ⱀⱀ Ⱁⱁ Ⱂⱂ Ⱃⱃ Ⱄⱄ Ⱅⱅ Ⱆⱆ Ⱇⱇ Ⱈⱈ Ⱉⱉ Ⱊⱊ Ⱋⱋ Ⱌⱌ Ⱍⱍ Ⱎⱎ Ⱏⱏ Ⱐⱐ Ⱑⱑ Ⱒⱒ Ⱓⱓ Ⱔⱔ Ⱕⱕ Ⱖⱖ Ⱗⱗ Ⱘⱘ Ⱙⱙ Ⱚⱚ Ⱛⱛ Ⱜⱜ Ⱝⱝ Ⱞⱞ
- Кириллица — А Б В Г Д ЕЄ Ж Ѕ ꙀЗ И ІЇ К Л М Н О П Р С Т ѸꙊ Ф Х Ѡ Ц Ч Ш Щ Ъ ЫꙐ Ь Ѣ Ю Ꙗ Ѥ Ѧ Ѫ Ѩ Ѭ Ѯ Ѱ Ѳ Ѵ
- Рунический
- старший футарк ᚠᚢᚦᚨᚱᚲᚷᚹᚺᚾᛁᛃ ᛇᛈᛉᛊᛏᛒᛖᛗᛚᛜᛞᛟ
- футорк ᚠᚢᚦᚩᚱᚳᚷᚹᚻᚾᛁᛄ ᛇᛈᛉᛋᛏᛒᛖᛗᛚᛝᛞᛟ ᚪᚫᚣᛠ
- младший футарк ᚢᚦᚬᚱᚴᚼᚾᛁᛅᛋᛏᛒᛘᛚᛦ/ᛧ
Кодировки
Любые кодовые таблицы всегда имеют какую-то упорядоченность, поэтому по умолчанию кодовая таблица — это тоже последовательность символов.
Календарь и время
Среди единиц измерения времени тоже можно встретить много последовательностей.
- названия месяцев:
- (ЯНВ) январь
- (ФЕВ) февраль
- (МАР) март
- (АПР) апрель
- (МАЙ) май
- (ИЮН) июнь
- (ИЮЛ) июль
- (АВГ) август
- (СЕН) сентябрь
- (ОКТ) октябрь
- (НОЯ) ноябрь
- (ДЕК) декабрь
- дни недели
- (ПН) понедельник
- (ВТ) вторник
- (СР) среда
- (ЧТ) четверг
- (ПТ) пятница
- (СБ) суббота
- (ВС) воскресенье
- единицы измерения времени: терция, секунда, минута, полчаса, час, сутки, неделя, декада, фортнайт, месяц, четверть, триместр, квартал, семестр, полугодие, год, олимпиада, пятилетка, десятилетие, индиктион, сарос, век, тысячелетие, галактический год, кальпа.
Ноты
Последовательность нот – одна из самых известных последовательностей. Детей в детском саду учат запоминать порядок нот при помощи вот такого стишка:
До, ре, ми, фа, соль, ля, си,
Села кошка на такси.
Заплатила сто рублей
И поехала в музей.
А котёнок зацепился
И бесплатно прокатился.
Игры
В играх часто карты или фигуры располагаются по старшинству.
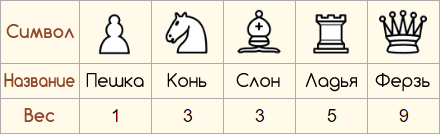
Шахматные фигуры
Игральные карты
Стандартная (французская) колода включает 54 карты: 52 основных, каждая из которых относится к одной из четырёх мастей (двух цветов) и имеет одно из 13 достоинств, и 2 специальные карты, так называемые джокеры, обычно различающиеся по рисунку. Для различных игр может использоваться как вся колода, так и её сокращённые варианты, не включающие джокеров:
- 52 карты (полная колода, от двоек до тузов);
- 36 карт (сокращённая колода, от шестёрок до тузов);
- 32 карты (малая колода, от семёрок до тузов);
- 24 карты (от девяток до тузов) — используется для игры в тысячу.
Обычно старшинство по возрастанию такое: 2,3,4,5,6,7,8,9,10,Валет(J),Дама(Q),Король(K),Туз(A). Самая сильная масть обычно крести ♣, затем вини ♠, черви ♥ и самая слабая буби ♦. В зависимости от игры, старшинство карт и мастей может меняться. Например, туз может быть как самой младшей картой, так и самой старшей в своей масти. А вот в игре в «козла» 6♣ старше, чем Д♣. В покере вообще важна комбинация карт. Старшинство комбинаций зависит от вероятности их выпадения — чем реже комбинация, тем она «дороже»: самая редкая — роял флэш.
Карты Таро
Стандартная колода состоит из 78 карт. Старшие арканы — козыри, обычно 22 карты. Младшие арканы — четыре масти (жезлы, кубки, мечи и пентакли), обычно 56 карт, по 14 карт каждой масти. Младшие арканы повторяют классическую колоду игральных карт, а вот старшие отличаются.
К старшим (или великим) арканам относятся 22 карты, каждая из которых имеет своё оригинальное название. В классическом (наиболее распространённом) варианте козыри имеют названия:
- (0 или XXII) «Дурак» («Шут»)
- (I) «Маг»
- (II) «Жрица»
- (III) «Императрица»
- (IV) «Император»
- (V) «Иерофант» («Первосвященник»)
- (VI) «Влюблённые» («Выбор»)
- (VII) «Колесница»
- (VIII) «Справедливость» («Правосудие»)
- (IX) «Отшельник»
- (X) «Колесо Фортуны»
- (XI) «Сила»
- (XII) «Повешенный»
- (XIII) «Смерть»
- (XIV) «Умеренность» («Время»)
- (XV) «Дьявол»
- (XVI) «Башня»
- (XVII) «Звезда»
- (XVIII) «Луна»
- (XIX) «Солнце»
- (XX) «Страшный суд» («Суд»)
- (XXI) «Мир»
Китайский гороскоп
В основе китайского гороскопа, используемого в Китае и других странах юго-восточной Азии, лежат 10- и 12-летний циклы.
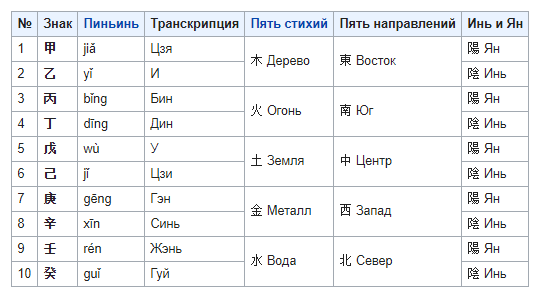
Небесные стволы — циклические знаки десятеричного цикла, использующиеся для календарных обозначений. По характеру использования иногда соответствует римским цифрам или любой другой системе исчисления на письме (а. б. в., 1) 2) 3) и т.п.).
Расположены в следующем порядке: 甲、乙、丙、丁、戊、己、庚、辛、壬、癸.
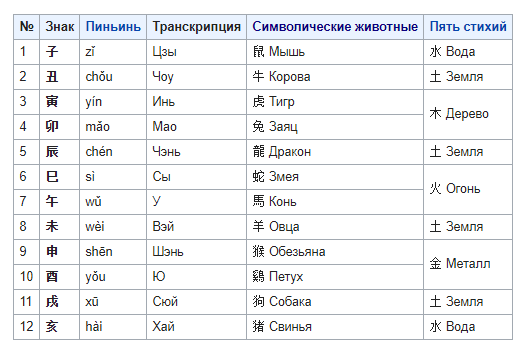
Земные ветви — циклические знаки двенадцатеричного цикла, используемые для ведения летоисчисления.
Расположены в следующей последовательности: 子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥
Им соответствуют символические животные: 鼠 Мышь, 牛 Корова, 虎 Тигр, 兔 Заяц, 龍 Дракон, 蛇 Змея, 馬 Конь, 羊 Овца, 猴 Обезьяна, 鷄 Петух, 狗 Собака, 猪 Свинья.
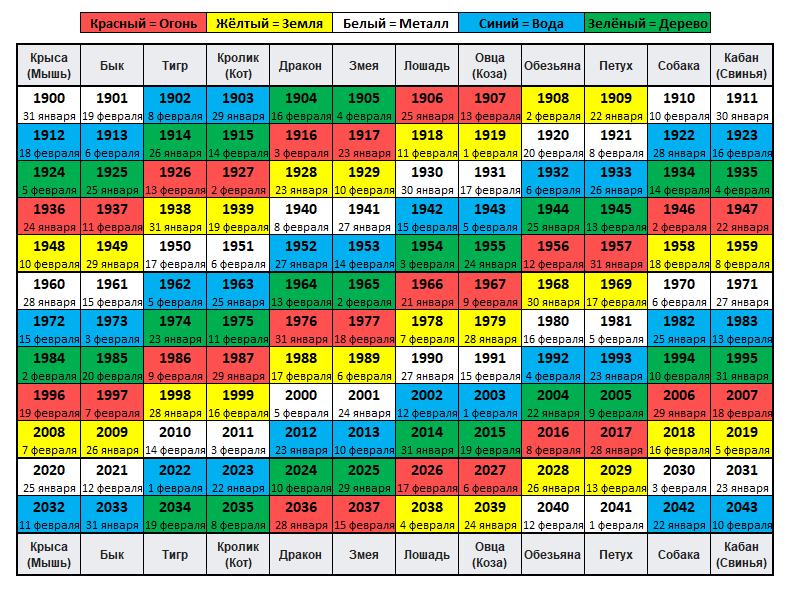
60-летний цикл является результатом взаимодействия 10-летнего и 12-летнего циклов. Каждый год характеризуется по инь/ян, по элементу и по животному. Например, начинается каждый цикл янской деревянной крысой и продолжается до следующей янской деревянной крысы. Чётность числа 12 приводит к тому, что каждое зодиакальное животное встречается только в одной форме инь/ян, например, дракон — всегда ян, а бык — всегда инь. Поэтому цикл длится именно 60 лет, а не 120.
Зодиакальные созвездия
А это перечень зодиакальных созвездий. Конечно, Солнце движется через них по кругу, поэтому последовательность можно начинать с любого созвездия. Но принято с того, в котором находится точка весеннего равноденствия, а это Овен. В классической астрологии используют 12 зодиакальных созвездий, но недавно стала популярна 13-знаковая астрология с новым знаком зодиака - Змееносцем.
- ♈ Овен
- ♉ Телец
- ♊ Близнецы
- ♋ Рак
- ♌ Лев
- ♍ Дева
- ♎ Весы
- ♏ Скорпион
- ⛎ (Змееносец)
- ♐ Стрелец
- ♑ Козерог
- ♒ Водолей
- ♓ Рыбы
Можно даже использовать не только классические европейские календари, но и другие, например, майя.
Или даже вот такие ![]()
Планеты
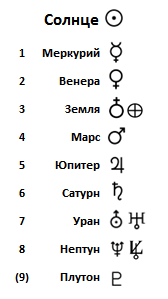
Планеты Солнечной системы расположены по удалению от Солнца в таком порядке:
Спутники планет (в порядке их открытия):
- Меркурий (0): –
- Венера (0): –
- Земля (1): Луна
- Марс (2): Фобос, Деймос
- Юпитер (50): Ио, Eвропа, Ганимед, Каллисто, Амальтея, Гималия, Элара, Пасифе, Синопе, Лиситея, Карме, Aнанке, Леда, Tеба, Aдрастея, Метида, Каллирое, Фемисто, Мегаклите, Тайгете, Халдене, Гарпалике, Калике, Иокасте, Эриноме, Исоное, Праксидике, Автоное, Тионе, Гермиппе, Этне, Эвридоме, Эванте, Эвпорие, Ортозие, Спонде, Кале, Пазифее, Гегемоне, Мнеме, Аойде, Тельксиное, Архе, Каллихоре, Гелике, Карпо, Эвкеладе, Киллене, Коре, Герсе
- Сатурн (53): Mимас, Энцелад, Teфия, Диона, Рея, Tитан, Гиперион, Япет, Феба, Янус, Эпиметей, Елена, Teлесто, Калипсо, Aтлас, Прометей, Пандора, Пан, Имир, Палиак, Тарвос, Иджирак, Суттунг, Кивиок, Мундилфари, Альбиорикс, Скади, Эррипо, Сиарнак, Трюм, Нарви, Мефона, Паллена, Полидевк, Дафнис, Эгир, Бефинд, Бергельмир, Бестла, Фарбаути, Фенрир, Форньот, Хати, Гирроккин, Кари, Логи, Сколл, Сурт, Анфа, Ярнсакса, Грейп, Таркек, Эгеон
- Уран (27): Aриэль, Умбриэль, Tитания, Oберон, Mирандa, Корделия, Oфелия, Бианка, Крессидa, Дездемона, Джульетта, Порция, Розалинда, Белинда, Пак, Калибан, Сикоракса, Просперо, Сетебос, Стефано, Тринкуло, Франциско, Маргарита, Фердинанд, Пердита, Маб, Купидон
- Нептун (13): Tритон, Нереида, Наяда, Таласса, Деспина, Галатея, Ларисса, Протей, Галимеда, Псамафа, Сао, Лаомедея, Несо
- Плутон (5): Харон, Никта, Гидра, Кербер, Стикс
Спектр
Порядок основных цветов в спектре: Красный, Оранжевый, Жёлтый, Зелёный, Голубой, Синий, Фиолетовый
Фраза для запоминания: Каждый Охотник Желает Знать Где Сидит Фазан.
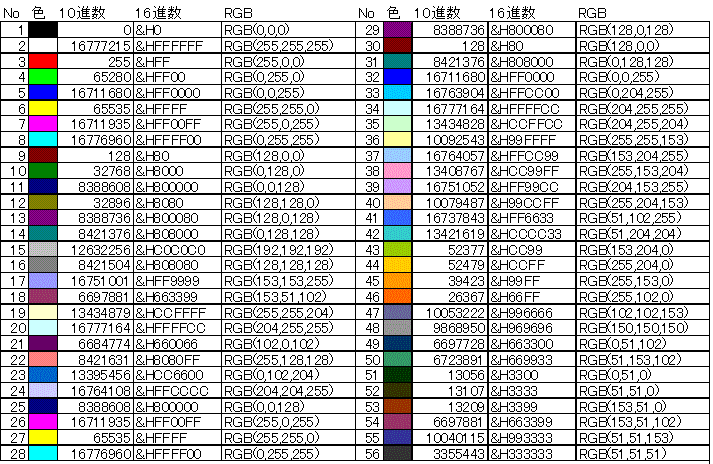
Последовательности цветов
Начиная с 2000 года Институт цвета Pantone объявляет один из цветов «Цветом года». Цвет выбирается на специальных секретных встречах, проходящих дважды в год в какой-либо из европейских столиц. После двух дней презентаций и обсуждений выбирается один цвет для следующего года. Например, цвет лета 2013 года был выбран весной 2012 года в Лондоне. Цвет призван олицетворять Дух времени; например, в презентации цвета 2011 года говорилось: «Во времена стресса нам нужно что-то для поднятия настроения. Жимолость — пленительный, стимулирующий цвет, вызывающий выброс адреналина, он идеально подходит для борьбы с хандрой.» Результаты встреч публикуются в журнале Pantone View, на который затем ссылаются дизайнеры одежды, флористы и другие ориентированные на потребителей компании, планирующие свои будущие продукты. В 2016 и 2021 годах были выбраны два цвета. Цветом 2025 года выбран Mocha Mousse «Мокка Мусс» — насыщенный карамельно-шоколадный оттенок, который сочетает роскошь и уют, природную теплоту и универсальность.
Такая последовательность цветов вполне себе последовательность. В качестве последовательности можно использовать и наименования цветов, и их цветовые координаты в различных цветовых моделях, и номера из каталога Pantone. И вообще, любые фиксированные палитры, не только порядок цветов в радуге – это тоже последовательности цветов. Например, цвета в палитре VBA:
Химические элементы
Гомологические ряды
В химии гомологическим рядом называют ряд химических соединений одного структурного типа, отличающихся друг от друга по составу на определённое число повторяющихся структурных единиц (так называемую гомологическую разность).
Например, гомологический ряд насыщенных углеводородов или парафинов (алканов) выглядит так:
Алканы: Метан (CH4), Этан (C2H6), Пропан (C3H8), Бутан/Изобутан, Пентан, Гексан, Гептан, Октан, Нонан, Декан, Ундекан, Додекан, Тридекан, Тетрадекан, Пентадекан, Гексадекан, Гептадекан, Октадекан, Нонадекан, Эйкозан, Генэйкозан, Докозан, Трикозан, Тетракозан, Пентакозан, Гексакозан, Гептакозан, Октакозан, Нонакозан, Триаконтан, Гентриаконтан, Дотриаконтан, Тритриаконтан, Тетратриаконтан, Пентатриаконтан, Гексатриаконтан, Гептатриаконтан, Октатриаконтан, Нонатриаконтан, Тетраконтан, Гентетраконтан, Дотетраконтан, Тритетраконтан, Тетратетраконтан, Пентатетраконтан, Гексатетраконтан, Гептатетраконтан, Октатетраконтан, Нонатетраконтан, Пентаконтан, Генпентаконтан, Допентаконтан, Трипентаконтан, Тетрапентаконтан, …, Гексаконтан, …, Гептаконтан, …, Гектан, …, Пентаконтагектан, …, Нонаконтатриктан (C390H782)
Общая формула алканов CnH2n+2.
Президенты США
- Джордж Вашингтон
- Джон Адамс
- Томас Джефферсон
- Джеймс Мэдисон
- Джеймс Монро
- Джон Куинси Адамс
- Эндрю Джексон
- Мартин Ван Бюрен
- Уильям Гаррисон
- Джон Тайлер
- Джеймс Нокс Полк
- Закари Тейлор
- Миллард Филлмор
- Франклин Пирс
- Джеймс Бьюкенен
- Авраам Линкольн
- Эндрю Джонсон
- Улисс Грант
- Ратерфорд Хейс
- Джеймс Гарфилд
- Честер Артур
- Гровер Кливленд
- Бенджамин Гаррисон
- Гровер Кливленд (второй раз)
- Уильям Мак-Кинли
- Теодор Рузвельт
- Уильям Тафт
- Вудро Вильсон
- Уоррен Гардинг
- Калвин Кулидж
- Герберт Гувер
- Франклин Рузвельт
- Гарри Трумэн
- Дуайт Эйзенхауэр
- Джон Кеннеди
- Линдон Джонсон
- Ричард Никсон
- Джеральд Форд
- Джимми Картер
- Рональд Рейган
- Джордж Герберт Уокер Буш («Джордж Буш — старший»)
- Билл Клинтон
- Джордж Уокер Буш («Джордж Буш — младший»)
- Барак Обама
- Дональд Трамп
- Джо Байден
- Дональд Трамп
ЧМ по футболу
- 1930
 Уругвай
Уругвай - 1934
 Италия
Италия - 1938
 Италия
Италия - 1950
 Уругвай
Уругвай - 1954
 Западная Германия
Западная Германия - 1958
 Бразилия
Бразилия - 1962
 Бразилия
Бразилия - 1966
 Англия
Англия - 1970
 Бразилия
Бразилия - 1974
 Западная Германия
Западная Германия - 1978
 Аргентина
Аргентина - 1982
 Италия
Италия - 1986
 Аргентина
Аргентина - 1990
 Западная Германия
Западная Германия - 1994
 Бразилия
Бразилия - 1998
 Франция
Франция - 2002
 Бразилия
Бразилия - 2006
 Италия
Италия - 2010
 Испания
Испания - 2014
 Германия
Германия - 2018
 Франция
Франция - 2022
 Катар
Катар
Не последовательности
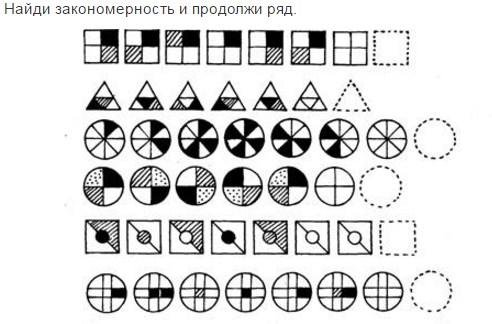
Некоторые задачи могут и не содержать последовательностей, как таковых. Тем не менее, в них присутствуют некие ряды элементов с определёнными закономерностями. Например, вот такая задачка:
На самом деле, если произвести полную декомпозицию задачи, то всё равно в конце концов придём к комбинации простых последовательностей атрибутов.
Другое
Можно привести ещё кучу последовательностей или перечислений тех или иных однородных вещей в определённом порядке. Например:
- порядок символов на клавиатуре: !"№;%:?*()_+ ЙЦУКЕНГШЩЗХЪ ФЫВАПРОЛДЖЭ ЯЧСМИТЬБЮ
- или в латинской раскладке: !@#$%^&*()_+ QWERTYUIOP{} ASDFGHJKL:"| ZXCVBNM<>?
- первые буквы названий чисел: одтчпшсвддодтчпшсвдд
- количество букв в названиях чисел: 4,3,3,6,4,5,4,6,6,6,11,10,10,12, …
- первые буквы месяцев и дней недели: ЯФМАМИИАСОНД – ПВСЧПСВ
- количество букв в названиях месяцев и дней недели: 6,7,4,6,3,4,4,7,8,7,6,7 – 11,7,5,7,7,7,11
- перечень 88-ми созвездий по алфавиту
- перечень штатов США по алфавиту
- перечень регионов России
- города, в которых проводились олимпиады, чемпионаты мира по футболу
- нобелевские лауреаты по физике
- фильмы, получившие Оскара
- гонщики-победители Формулы-1
- названия годовщин свадьбы
- последовательности исторических событий
- различные рейтинги и топ-листы
- таблицы производительности или линейки выпуска изделий
- последовательности нуклеотидов в ДНК
- слова по порядку из любого известного произведения, где была чёткая известная последовательность событий:
- Сказка «Репка»: дед, бабка, внучка, Жучка, кошка, мышка
- Считалочка: раз, два, три, четыре, пять, вышел, зайчик, погулять, вдруг, охотник, выбегает, прямо, в, зайчика, стреляет, …
- Считалочка: На златом крыльце сидели царь, царевич, король, королевич, сапожник, портной…
- Стишок про 10 негритят: поперхнулся, не проснулся, не возвратился, зарубился, ужалил шмель, засудили, попался на приманку, схватил медведь, сгорел, повесился
- Ночь, улица, фонарь, аптека…
- тарифы на трехтарифном счётчике Т1 (пик), Т2 (ночь), Т3 (полупик)
- …
Кстати, последовательность символов на этой страничке – это тоже последовательность. Поэтому даже просто перечислить всё – это уже непосильная задача. Но основные последовательности, которые можно использовать в задачах и головоломках, я надеюсь, вспомнил.
Пример
Хорошим примером использования последовательностей служит вот этот сайт:
- https://ru.hacktest.net/ – хакерский тест
Это своеобразная веболомка, состоящая из набора задач. Всего 23 уровня (шага). На каждом шаге нужно найти ответ к следующему по порядку шагу, причём ответ представляет собой следующий член последовательности к слову, расположенному на текущем шаге. Ответ вводится в специальном поле ввода. Бывают подсказки.
Например, если на пятом шаге была загадана «пятница», то для перехода на шестой шаг надо ответить «суббота», а если был загадан «май», то ответить надо – «июнь». На каждом шаге множество вариантов загадывания, и головоломка до сих пор пополняется заданиями, так что при каждом новом прохождении попадаются всё новые и новые вопросы. Очень интересный сайт, рекомендую.
- https://diary.ru/~mayou/p103732403_otvety-na-hakerskij-test.htm – здесь собраны ответы на «хакерский тест» выше