• Онлайн: 2
Содержание
Бинарные изображения
В компьютерном мире существует такой термин как "бинарное изображение" — разновидность цифровых растровых изображений, когда каждый пиксел может представлять только один из двух цветов, например, чёрный и белый.
Значения каждого пиксела условно кодируются как «0» и «1». Значение «0» условно называют задним планом или фоном (англ. background), а «1» — передним планом (англ. foreground).
Домик
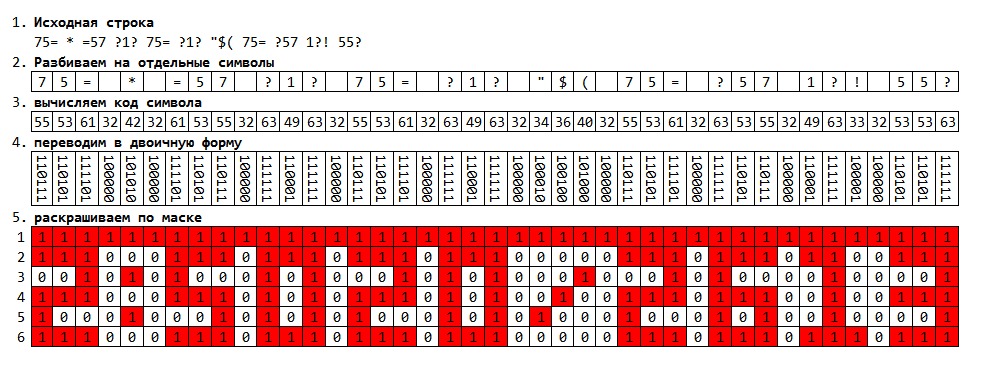
Когда мы видим перед собой уже нарисованную картинку с домиком, то сразу понятно, что это дом. Но когда видим соответствующую этой картинке бинарную маску, то уже не всё так понятно. А уж если эти нолики с единичками перевести в восьмеричную, десятичную или шестнадцатиричную систему счисления, то ни о какой картинке с домиком уже речи нет — она будет надёжно «скрыта» от глаз, при том, что информация о ней никуда не денется, просто она станет закодирована.
Можно сделать ещё «хуже» — каждому шестнадцатеричному коду строки изображения сопоставить графический символ из какой-либо известной кодовой таблицы, например, windows-1251 или CP866. Тогда каждая строчка такого изображения будет кодироваться всего одним символом, и всё изображение с домиком превратится в «→&BяBZZ~».
Можно даже не кодировать каждую строку, а просто выписать их друг за другом по отдельности или «сплошняком». В этом случае тоже непросто понять, что закодировано именно изображение.
Фидошный адрес
Все эти способы преобразования и хранения бинарных изображений активно используются в компьютерной технике, что не мешает использовать их в задачах и головоломках. Однажды один фидошник прислал мне такую задачу:
Если честно, то я очень долго думал над этой задачей, пробовал применять разные шифры перестановки, и замены, пробовал их комбинировать — но не получалось. Потом всё же начал с самого начала и подробнее прочитал условие. Подсказка была в самом начале: «компьютерная графика». Стал думать, какие способы есть перевести число в графику. Вначале подумал, что тройки символов - это координаты в пространстве, потом попробовал определить позиции символов и построить по их номерам гистограмму. В конце концов, решил применить метод бинарных изображений, изложенный выше — и получилось! Тоже не с первого раза, конечно :)
На картинке получился адрес моего фидошного узла 2:5020/2613. Почему сверху вышла сплошная полоска? Если бы автор задачки попытался использовать пятизначные двоичные числа, то попал бы в самую верхнюю часть кодовой таблицы с кодами от 0 до 32, а там не во всех таблицах есть отображаемые символы, чаще — управляющие. Поэтому он сделал сдвиг на две строки вниз (на 32 символа). В двоичном виде это получилось так, как будто к числу прибавили 100000 (3210=1000002), вот в каждой строчке и появилась лишняя единичка. Ничего страшного, информация при этом не потерялась. Прекрасная задачка! ![]()
Космические послания
Продолжение см. Космические послания
Ссылки
- https://habr.com/ru/post/416177/ — Формула Таппера и реализация алгоритма на Python
- Бинарное_изображение — Статья на Википедии