• Онлайн: 2
Содержание
Перестановочные шифры
Это описание перестановочных шифров для начинающих составителей головоломок.
Простая перестановка
Простая перестановка без ключа — один из самых простых методов шифрования. Буквы перемешиваются по каким-либо правилам, но эти правила могут быть разными — и простыми и сложными.
Транспозиция
Допустим, у нас есть фраза: «МОЖНО, НО НЕЛЬЗЯ». И мы хотим её зашифровать. Самый простой способ - это записать всю фразу задом наперёд: «ЯЗЬЛЕН ОН, ОНЖОМ». Можно порядок слов в предложении оставить исходным, но каждое слово записать задом наперёд: «ОНЖОМ, ОН ЯЗЬЛЕН». А можно менять местами каждые две буквы: «ОМНЖ,ООНЕНЬЛЯЗ». Это называется «транспозиция» или простая перестановка в чистом виде.

Транспонирование
В этом шифре используется таблица. Сообщение записывается в таблицу по строкам, а для образования шифрованного текста считывается по столбцам. Ну или наоборот - записывается на столбцам, а считывается по строкам. Мы как бы переворачиваем таблицу относительно её диагонали, проходящей через верхний левый и нижний правый углы. Математики называют такой способ переворота таблицы транспонированием.
Для шифрования нужно нарисовать подходящего размера таблицу, вписать туда построчно шифруемый текст, а затем выписать его по столбцам в одну строку. Для расшифровки нужно лишь будет сообщить ключ шифра в виде размера таблицы. На рисунке ниже из ABCDEFGHIJKL получается ADGJBEHKCFIL. Согласитесь, понять без картинки, что это был алфавит, уже практически невозможно.
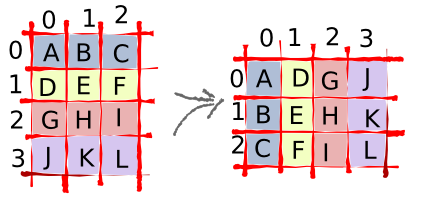
Итак, например, нам нужно зашифровать текст «Я памятник себе воздвиг нерукотворный, к нему не зарастёт народная тропа». В нём 72 символа. 72 - удобное число, оно делится без остатка на 2,4,6,8,12,18,24,36, поэтому можно использовать таблицы 2х36, 3х24, 4х18, 6х12, 8х9, 9х8, 12х6, 18х4, 24х3, 36х2 :). Определяемся с ключом (размером таблицы), вписываем текст по строкам, а затем переписываем его по столбцам.
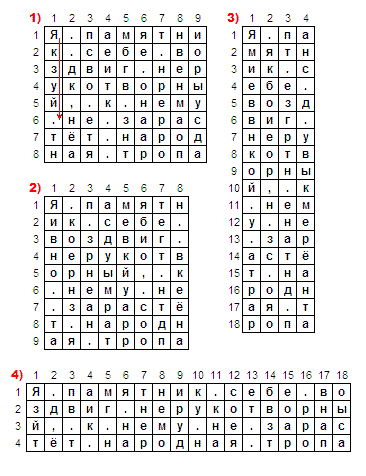
На рисунке выше показаны варианты с таблицами 9×8, 8×9, 4×18 и 18×4. Для третьего варианта (таблица 4×18) получится вот такой текст:
«Ямиеввнкой у атрар якбоиеор,н зс ояопт езгртн енатнд панс д увыкмерёанта (4:18)»
В данном случае я взял текст «как есть», то есть с пропусками между словами и со знаками препинания. Но если текст осмысленный, то знаки препинания и пропуски между словами можно и не использовать.
Штакетник
Упрощённый вариант транспонирования (с двухстрочной таблицей) - «штакетник». Напоминает «по конструкции» забор-шахматку.

Это очень простой способ шифровки, часто применяемый школьниками. Фраза записывается в две строки: в верхней пишутся нечётные буквы, в нижней - чётные. Затем нужно выписать подряд сначала верхнюю строку, затем нижнюю. Такое шифрование легко проделать и в уме, не выписывая сначала две строки.
«Я памятник себе воздвиг нерукотворный» превращается в «ЯАЯНКЕЕОДИНРКТОНЙ ПМТИСБВЗВГЕУОВРЫ».
Скитала
Известно, что в V веке до нашей эры правители Спарты, наиболее воинственного из греческих государств, имели хорошо отработанную систему секретной военной связи и шифровали свои послания с помощью «скиталы», первого простейшего криптографического устройства, реализующего метод простой перестановки.

Шифрование выполнялось следующим образом. На стержень цилиндрической формы, который и назывался «скитала», наматывали спиралью (виток к витку) полоску пергамента и писали на ней вдоль стержня несколько строк текста сообщения. Затем снимали со стержня полоску пергамента с написанным текстом. Буквы на этой полоске оказывались расположенными хаотично. Для восстановления текста требовалась скитала такого же диаметра.
По сути скитала - это наша обычная плоская таблица, обёрнутая вокруг цилиндра.
Считается, что автором способа взлома шифра скиталы является Аристотель, который наматывал ленту на конусообразную палку до тех пор, пока не появлялись читаемые куски текста. Изначально древний аппарат использовался в качестве сохранения секретных рецептов. Сейчас вместо узкой полоски пергамента можно использовать серпантин, а роль скиталы выполнит карандаш.
Сдвиг
Похожий результат можно получить, если буквы сообщения писать через определенное число позиций до тех пор, пока не будет исчерпан весь текст. Ниже пример готовой головоломки, составленной по таким правилам. «Три дробь четыре» - это подсказка, что зашифровано три слова, читать надо каждую четвёртую букву (4-8-12-16-..), по достижению конца переходить снова к началу со сдвигом на 1 букву влево (3-7-11-15-..) и т.д. На рисунке ниже зашифровано «Идите назначенным маршрутом».

Одиночная перестановка по ключу
Более практический метод шифрования, называемый одиночной перестановкой по ключу, очень похож на предыдущий. Он отличается лишь тем, что колонки таблицы не сдвигаются, а переставляются по ключевому слову, фразе или набору чисел длиной в строку таблицы. Кодируемая фраза записывается в подходящую таблицу построчно. Затем над таблицей вставляется пустая строка и в неё вписывается ключевое слово/фраза/последовательность чисел. Затем это ключевое слово/фраза/последовательность сортируется по алфавиту/значению, вместе с ней сортируются столбцы, тем самым перемешивая всю таблицу. Затем зашифрованная фраза выписывается построчно из этой перемешанной таблицы.
Например, можно сделать головоломку на основе судоку. Разгадывающему даётся текст «-УРОМКУЛО ЬУЁЗЕБЯДЛ НЗЯАТЛЫЙА ЦЬБАДНЕПУ ЕММДНИТОЁ ИЧТЮКЬНОО УНЁЙВЫЧЁС ХИЕПОТОДЦ ПРМГОУИК-» и предлагается решить судоку, в которой одна из строк помечена.
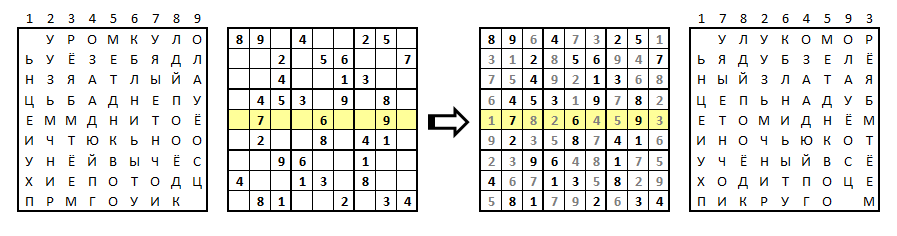
Решать эту головоломку придётся так: сначала нужно записать текст в таблицу 9×9, затем разгадать судоку, нарисовать пустую таблицу 9×9, надписать над ней ключевую строку из помеченной строки, и затем в таблицу под номерами вписать столбцы согласно их порядковым номерам в исходной таблице.
Для детей можно использовать этот же метод, но попроще, даже без цифр, а сразу нарисовав порядок перестановки в виде путей.

Двойная перестановка
Для дополнительной скрытности можно повторно шифровать сообщение, которое уже было зашифровано. Этот способ известен под названием «двойная перестановка». Для этого размер второй таблицы подбирают так, чтобы длины её строк и столбцов были не такие, как в первой таблице. Лучше всего, если они будут взаимно простыми. Кроме того, в первой таблице можно переставлять столбцы, а во второй строки.
Маршрутная перестановка
Обычное транспонирование таблицы (заполняем по строкам, читаем по столбцам) можно усложнить и считывать не по столбцам, а змейкой, зигзагом, по спирали или каким-то другим способом, т.е. задавать маршрут обхода таблицы. Такие способы заполнения таблицы если и не усиливают стойкость шифра, то делают процесс шифрования гораздо более занимательным. Правда, процесс расшифровки при этом усложняется, особенно, если маршрут неизвестен, и его ещё надо узнать.

На рисунке сверху последовательность символов «АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ.,?» вписана построчно в таблицу 6×6, а затем считана по маршруту, указанному линиями. Получаются следующие шифровки:
- АЁЛСЧЭБЖМТШЮВЗНУЩЯГИОФЪ.ДЙПХЫ,ЕКРЦЬ?
- АЁЛСЧЭЮЯ.,?ЬЦРКЕДГВБЖМТШЩЪЫХПЙИЗНУФО
- АБЁЛЖВГЗМСЧТНИДЕЙОУШЭЮЩФПКРХЪЯ.ЫЦЬ,?
- АЁЛСЧЭЮШТМЖБВЗНУЩЯ.ЪФОИГДЙПХЫ,?ЬЦРКЕ
- НЗВБАЁЖМЛСТШЧЭЮЯЩУФЪ.,?ЬЫХЦРПЙКЕДГИО
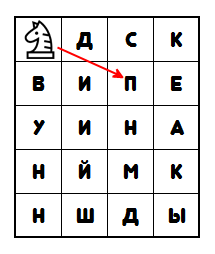
А здесь нужно обходить таблицу «ходом коня», причём маршрут уже нарисован, так что это совсем для маленьких :)
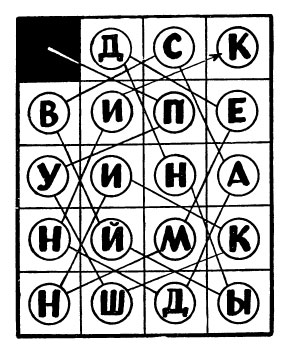
Но если подать эту головоломку так, как показано ниже, то будет уже совсем не просто, так как вариантов обхода ходом коня может быть много, и нужно будет найти из всех этих вариантов единственный правильный (ниже зашифровано «Пушкин. Медный всадник»).
Ещё один метод загадать маршрут - использовать мнемоническое стихотворение, в котором некими ключевыми словами заданы координаты обхода сетки. Допустим, есть шахматная доска, которую ходом шахматного коня нужно всю обойти клетка за клеткой так, чтобы побывать на каждой клетке только один раз. В результате получится маршрут длиной 64. Один из многих миллионов таких маршрутов показан на картинке ниже. Если в порядке обхода клеток вписать сообщение, то чтобы его разгадать, нужно будет восстановить этот самый маршрут.
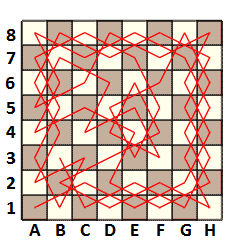
А вот загадать этот маршрут можно, например, вот таким стихотворением:
Алеет Осень Ценными Дарами, Еще Один Животворящий День. Хлеба Червонят Желтыми Шнурами, Хрустальных Вод Философична Сень. Два Вечера Цеплявшиеся Шишки Артист Писал, Бездонна Синева. Дорожный Шлак Целуют Червячишки, Еще Покрыта Флоксами Трава. Дымится Чай Эффектней Шоколада, Фарфоры Чашек Достаются Трем, Блондинке Девушка Дана Отрада Форшмак Делить Холодным Острием. Жена, Толкая Хилую Подругу, Желает Сняться Этим Выходным, Ценя Сама Арктическую Вьюгу, Бросает Шар Арбуза Четверым. Цикад Пяток, Едва Чревовещая, Дарует Дрему Фикусам Окна. Хотя Довольны Жаждавшие Чая, Хозяин Шумно Жертвует Вина. Фокстротами Шесть Девушек Пленились, Эстрадных Танцев Фантастичней Па, Едва Ступающий Цыпленок Вылез, А Селезень Блуждающий Пропал. Алеет Тело Бронзовой Осины, Царит Теней Ажурная Длина. Беззвучней, Чем Автомобиля Шины, Болоту Ветер Дарит Семена. Фонарь Восьмью Химерами Сияет, Жук Прилетает, Хлопая, Туда. Желанна Осень, Если Довершает Ценнейший Отдых Бодрого Труда.
Разгадывать его придётся так: «Алеет Осень» - это А1 (А Один), «Ценными Дарами» - C2 (Цэ Два), «Ещё Один» - E1 (E Один), «Животворящий День» - G2 (Жэ Два) и т.д.
Перестановка "Волшебный квадрат"
Волшебными (или магическими) квадратами называются квадратные таблицы со вписанными в их клетки последовательными натуральными числами от 1 до n2 (где n - размерность квадрата), которые дают в сумме по каждому столбцу, каждой строке и каждой диагонали одно и то же число.
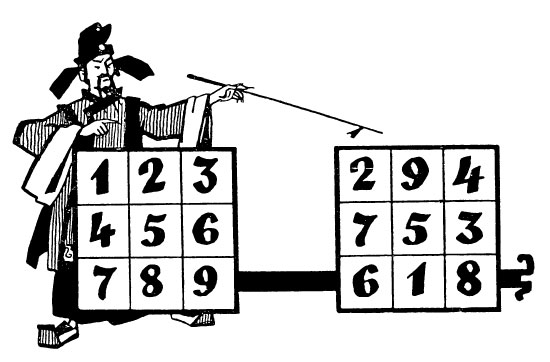
В известном ещё в Древнем Китае квадрате Ло-Шу третьего порядка (3×3) константа квадрата 15 повторяется 8 раз:
- по трём горизонталям: 2+9+4 = 7+5+3 = 6+1+8 = 15
- по трём вертикалям: 2+7+6 = 9+5+1 = 4+3+8 = 15
- по двум диагоналям: 2+5+8 = 4+5+6 = 15
Кстати, константу нечетного квадрата легко посчитать, умножив среднее число ряда, из которого составлен квадрат, на порядок квадрата. Для квадрата 3-го порядка (3×3) константа равна 123456789*3=15.
Итак, у нас вначале есть квадрат с числами по порядку, а затем, когда из них составлен «магический» квадрат, цифры идут уже не по порядку. Это и используют при шифровании.
Чтобы зашифровать какое-то послание, нужно сначала подобрать или составить подходящий по размеру волшебный квадрат, затем нарисовать пустую таблицу такого же размера, и вписать буквы текста по очереди в таблицу в соответствии с номерами в волшебном квадрате. Затем выписывают построчно буквы из таблицы в одну длинную строку. Порядок квадрата должен быть равен округлённому в большую сторону корню из длины шифруемой строки, чтобы строка полностью вошла в квадрат. Если строка короче, то остаток можно заполнить произвольными буквами или цифрами.
На первый взгляд кажется, будто магических квадратов очень мало. Тем не менее, их число очень быстро возрастает с увеличением размера квадрата. Так, существует лишь один магический квадрат размером 3х3, если не принимать во внимание его повороты и отражения. Счёт волшебным квадратам 4-го порядка уже идёт на сотни, 5-го - на сотни тысяч. Поэтому магические квадраты больших размеров могли быть хорошей основой для надежной системы шифрования того времени (в Древнем Китае), так как ручной перебор всех вариантов ключа для этого шифра был немыслим.
Метод террас
Есть очень простой метод составления нечётных волшебных квадратов, т.е. размером 3×3, 5×5, 7×7 и т.д. Это метод «террас» или «пирамидок».
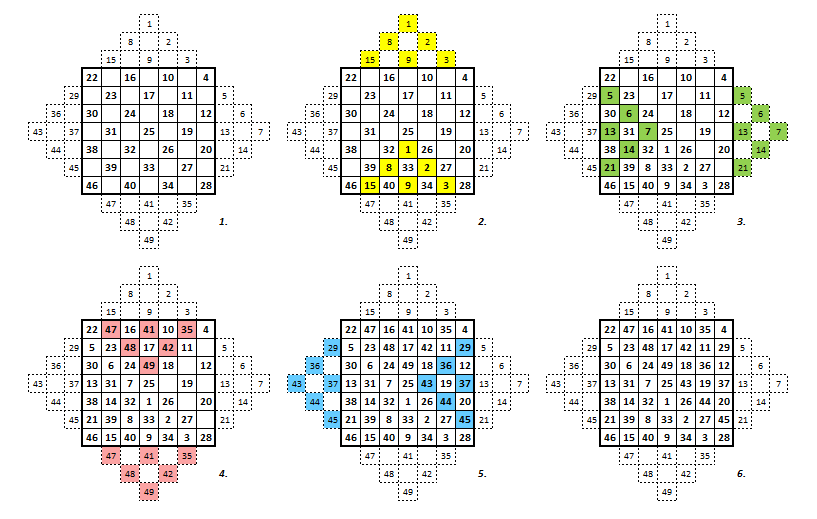
Рисуется квадрат нужного размера и к нему пририсовываются ступенчатые «террасы» (обозначены пунктиром). Далее по диагоналям сверху вниз направо квадрат заполняется последовательными числами. После этого «террасы» переносятся внутрь квадрата: правые - налево, левые - направо, верхние - вниз, а нижние - наверх. Получается волшебный квадрат!
На базе этого метода можно составлять разные головоломки. Если использовать метод напрямую, то получится вот такая головоломка:

Чтобы решить эту головоломку, нужно буквы из «террас» перенести в квадрат, тогда в квадрате прочитается полное сообщение. Здесь зашифрована фраза «За мостом засада, пройти нельзя, переходите речку в брод.»
А если использовать метод наоборот, то получится головоломка типа такой.
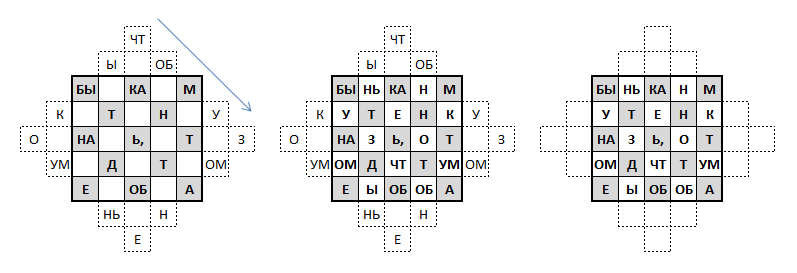
Чтобы её решить, надо вытащить соответствующие буквы из квадрата в «террасы».
Для квадратов 4×4, 6×6 и т.д. таких простых способов их составления не существует, поэтому проще использовать готовые. Например, квадрат Дюрера.

Вращающаяся решётка
Классическая решётка Кардано позволяет скрыть шифровку внутри мусорного текста и является хорошим примером стеганографии. Но если решётку Кардано использовать в качестве ключа для перестановочного шифра, то получим новый метод шифрования — вращающуюся решётку или сетку.
Решётка — это квадрат размером NxN клеток, некоторые из которых вырезаны. Вырезанные клетки могут касаться друг друга, в том числе вершинами, и даже сторонами. В одной клетке — одна буква. Вырезанные клетки должны располагаться таким образом, чтобы никакие две из них не оказывались в одном и том же месте при поворотах решётки.
При помощи конструктора, изображённого ниже, можно изготовить 416 (4 294 967 296) таких решёток. Для этого нужно вырезать строго одно из четырёх повторяющихся чисел. Для шифрования без мусора нужно вырезать все номера от 1 до 16, всего 16 клеток. Для шифрования с мусором некоторые числа можно не вырезать, оставшиеся места после шифрования заполнить любыми произвольными буквами, это и будет мусор.
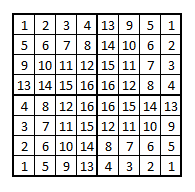
Использовать полученную решётку надо следующим образом. Положить решётку на бумагу и в вырезанные клетки по одной букве начать вписывать шифруемый текст. Как только 16 букв будет вписано, решётка поворачивается на 90°, и вписываются следующие 16 букв, и так ещё два раза. В результате будет вписано 64 буквы. Если текст был короче, то в оставшиеся на бумаге пустые места нужно вписать произвольные буквы. Более длинный текст можно разбить на части по 64, и шифровать каждую отдельно. А можно вписывать в окошки и по две буквы.
Есть второй способ перекладывания решётки во время шифрования — не поворачивать решётку на 90° три раза, а в первый раз повернуть её на 180°, второй раз перевернуть обратной стороной относительно горизонтальной оси, в третий раз - снова повернуть на 180°.
Это были перестановочные шифры. А теперь можно почитать про Шифры замены.

