• Онлайн: 2
Содержание
Математика с картинками
Математика - это не только формулы и числа. Очень часто это ещё и схемы, и графы, и чертежи. К примеру, многие арифметические задачи можно иллюстрировать. Например, вместо 3+5=8 нарисовать две кучки яблок по 3 и 5 штук, а затем большую, в которой 8 яблок. Но это не та «математика с картинками», о которой я хочу написать. Существует множество топологических и геометрических задач, в которых просто не обойтись без рисунков и чертежей. Расскажу о некоторых из них.
Из теории графов
Задача Эйлера о семи мостах
Вот пример классической задачи из теории графов. Это старинная математическая задача, в которой спрашивалось, как можно пройти по всем семи мостам Кёнигсберга, не проходя ни по одному из них дважды. Мосты располагались вот так.

Многие пытались решить эту задачу как теоретически, так и практически, прогуливаясь по Кёнигсбергу (нынешнему Калининграду), но никому так и не удалось её решить, пока за это не взялся математик Леонард Эйлер. Он взял карту города, отметил на ней точки на каждом берегу и на каждом острове, а затем соединил их линиями. Получился граф. На упрощённой схеме города (графе) мостам соответствуют линии (ребра графа), а частям города — точки соединения линий (вершины графа). После этого математик стал думать над задачей.
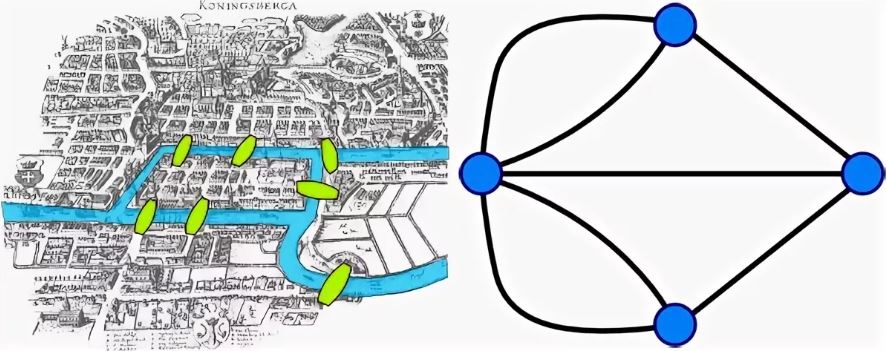
В ходе рассуждений Эйлер пришёл к следующим выводам:
- Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин.
- Если все вершины графа чётные, то можно начертить этот граф без отрыва карандаша от бумаги, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
- Если ровно две вершины графа нечётные, то можно начертить этот граф без отрыва карандаша от бумаги, при этом нужно начинать с одной из нечётных вершин и завершить его в другой нечётной вершине.
- Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
Граф кёнигсбергских мостов имел четыре нечётные вершины (то есть все) — следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.
Одним росчерком
Задача Эйлера - это классический пример задач из серии «нарисуй фигуру одним росчерком». В этих задачах нужно нарисовать заданную фигуру, не отрывая пера (карандаша, ручки, фломастера, светового пера, стилуса…) от бумаги.
Например, вот такие фигуры:
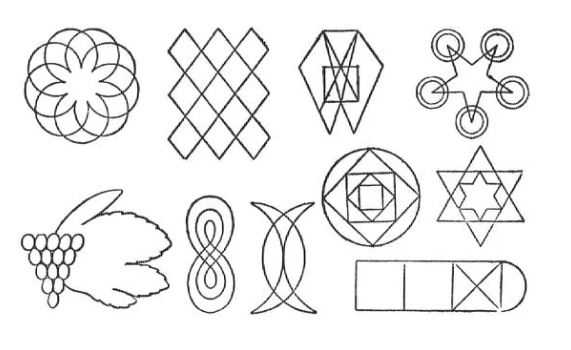
Благодаря Эйлеру проверить, возможно ли это сделать, очень легко. Нужно просто посчитать количество лучей, исходящих из из каждого узла. Если все узлы чётные, то можно начинать рисовать фигуру из любой точки. Если два узла нечётных, то начинать нужно в одном из них, а заканчивать в другом. Если нечётных узлов больше двух, то одним росчерком нарисовать фигуру невозможно.
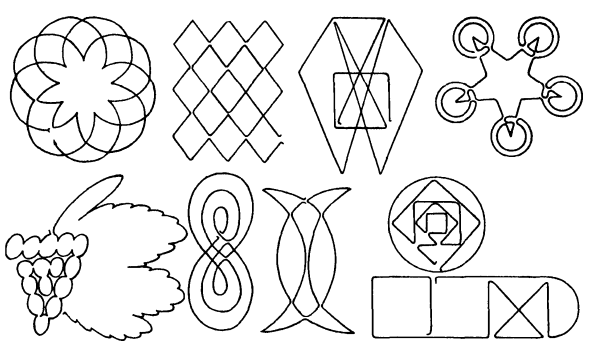
На рисунке выше приведены решения задачек с предыдущего рисунка. «Звезду Давида» попробуйте нарисовать сами :)
Задача о четырёх красках
Математики любят доказывать всякие теоремы. Одна из них - «о четырёх красках». Умные математики подумали-подумали и доказали, что любую карту можно раскрасить всего 4-мя красками так, что никакие две области, имеющие общую границу, не будут одного цвета.
Но одно дело доказать, а другое - сделать! Не у каждого получается с первого раза подтвердить эту теорию на практике. Поэтому до сих пор появляются задачки на раскраску карт. Иногда очень красивые. Это даже не задачи, а скорее антистресс-раскраски.
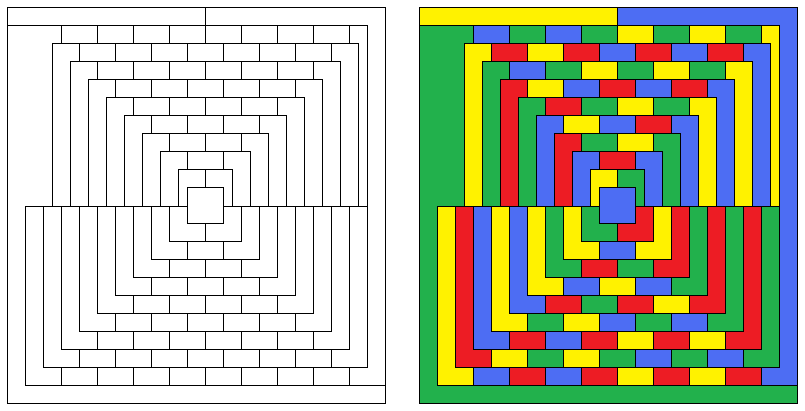

Пространственные задачи
Сколько надо кубиков?
На рисунке ниже вы видите объёмную фигуру, которая собрана из кубиков. Необходимо соединить концы данной фигуры с помощью минимального количества таких же кубиков. Сколько кубиков для этого понадобится?
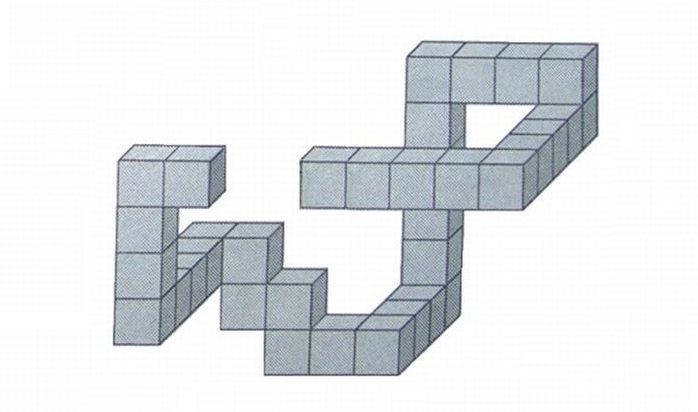
Для того, чтобы решить эту задачу, нужно немного логики и хорошее пространственное воображение. Правильный ответ ниже.

