• Онлайн: 2
Четверичный шифр
Если увлекаться одновременно программированием, криптографией, математикой и ММЦК, как вы думаете, что может прийти в голову? Конечно, придумать шифр из множества маленьких цветных кусочков!
Однажды я посмотрел на логотип всем известной операционной системы и мне вдруг подумалось…
- `2*2 = 4 `, то есть квадрат 2х2 состоит из 4-х квадратов
- Число размещений n объектов на k местах без повторений `A_n^k = (n!)/((n-k)!) = ` ` (4!)/((4-4)!) = (4!)/(0!) = ` `(1*2*3*4)/1 = 24 `, значит, вариантов логотипа может быть аж 24 штуки.
- А вот число размещений с повторениями `bar(A)_n^k = n^k = 4^4 = 256 `. И это значит, что цветные квадратики в квадрате 2х2 с повторами цветов можно расположить 256-ю разными способами.
- ну и в-четвёртых, вспомнилось, что в 8-битных кодовых таблицах тоже `256 ` символов.
В заключение этих моих размышлений подумалось, а почему бы каждый символ из 8-битной кодовой таблицы не закодировать одним из таких цветных 4-х цветных квадратиков 2х2? Их же тоже 256. Надо попробовать!
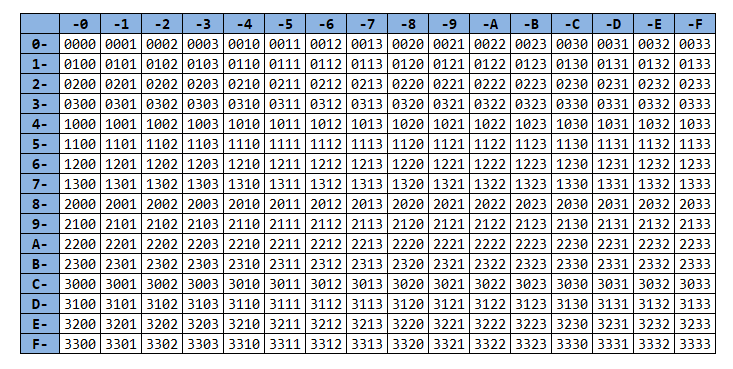
Перебрать все 256 вариантов из 4-х цветов очень просто. Временно вместо цветов берём цифры 0,1,2,3, а это, между прочим, цифры четверичной системы счисления. Значит, если просто напечатать в цикле 256 порядковых чисел, переводя их из десятичной в четверичную систему, то и получим все нужные нам размещения с повторениями. Затем каждое четверичное число размещаем в квадратиках, а затем раскрашиваем, как картины по номерам – дело простое :)
Вот так выглядят все 256 четверичных чисел:
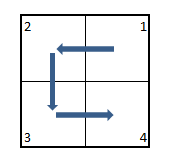
Размещаем их в квадратиках, например, вот в таком порядке:
Получаем заготовку для раскраски:
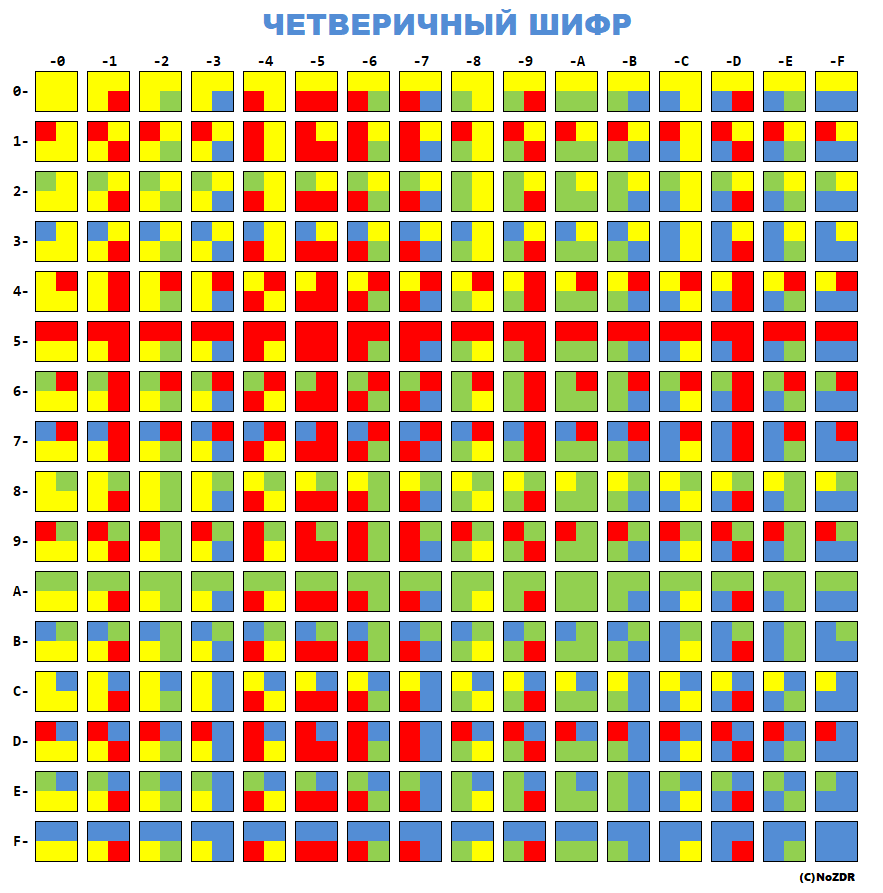
А теперь красим в 4 цвета: 0-жёлтый, 1-красный, 2-зелёный, 3-синий:
и мы получили готовую кодовую таблицу для шифрования. Учитывая, что кодируется вся таблица, такими квадратиками можно закодировать не только текст, а вообще любой 16-ричный код.
И логотип наш оказался на месте 9Сh или 156. В Windows-1251 это место буквы њ – буквы расширенной кириллицы, 17-й буквы сербского и 18-й буквы македонского алфавитов.
Попробуйте, используя таблицу windows-1251 и таблицу четверичного шифра расшифровать, что здесь зашифровано:
А ответить можно на канале ММЦК: https://t.me/colorbits/11