Число π

π (произносится «пи») — математическая постоянная, равная отношению длины окружности к её диаметру. Обозначается буквой греческого алфавита «π».

Впервые обозначением этого числа греческой буквой π воспользовался британский математик Уильям Джонс в 1706 году, а общепринятым оно стало после работ Леонарда Эйлера в 1737 году. Это обозначение происходит от начальной буквы греческих слов περίμετρος περιφέρεια — периметр окружности (периферии).

Как считают специалисты, это число было открыто ещё в Вавилоне. Оно использовалось при строительстве знаменитой Вавилонской башни. Однако, недостаточно точное исчисление значения «Пи» привело к краху всего проекта. Возможно, что эта математическая константа лежала в основе строительства легендарного Храма царя Соломона. Исследование числа π и уточнение его значения шли параллельно с развитием всей математики и занимают несколько тысячелетий. Сначала π изучалось с позиции геометрии, затем развитие математического анализа в XVII веке показало универсальность этого числа.

14 марта в мире отмечается один из самых необычных праздников — Международный день числа «Пи» (International Pi Day). Впервые День был отмечен в 1988 году в научно-популярном музее Эксплораториум в Сан-Франциско (San Francisco Exploratorium), а придумал этот неофициальный праздник годом ранее физик из Сан-Франциско Ларри Шоу, который подметил, что в американской системе записи дат (месяц / число) день 14 марта — 3/14 — совпадает с первыми разрядами числа π = 3,14… Примечательно, что Международный день числа «Пи», случайно или умышленно, совпадает с днем рождения одного из наиболее выдающихся физиков современности — днем рождения Альберта Эйнштейна (Albert Einstein, 1879—1955).

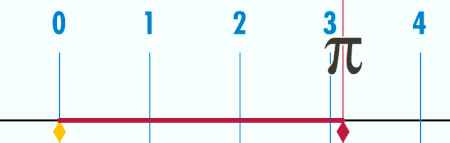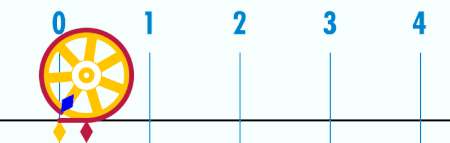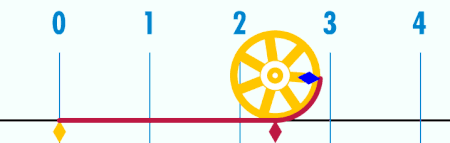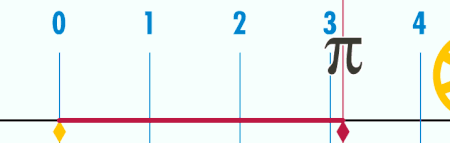
Если диаметр окружности равен единице, то длина окружности — это число «пи». Это легко понять, посмотрев на ролик ниже:

Число π иррационально, то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. Иррациональность числа π была впервые доказана Иоганном Ламбертом в 1761 году путём разложения тангенса в непрерывную дробь. В 1794 году Лежандр привёл более строгое доказательство иррациональности чисел π и π².

Число π с первой тысячей высших разрядов десятичной дроби:

3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989

На июнь 2022 года были известны первые 100 триллионов знаков числа π после запятой. Сейчас уже, наверное, больше :)

Помимо того, что π число иррациональное, оно ещё и трансцендентное, то есть оно не может быть корнем какого-либо многочлена с целыми коэффициентами. Трансцендентность числа π была доказана в 1882 году профессором Кёнигсбергского, а позже Мюнхенского университета Линдеманом. Доказательство упростил Феликс Клейн в 1894 году. Поскольку в евклидовой геометрии площадь круга и длина окружности являются функциями числа π, то доказательство трансцендентности π положило конец попыткам построить квадратуру круга, длившимся более 2,5 тысяч лет.

Квадратура круга — это задача, заключающаяся в нахождении способа построения с помощью циркуля и линейки (без шкалы с делениями) квадрата, равновеликого по площади данному кругу. Наряду с трисекцией угла и удвоением куба, квадратура круга является одной из самых известных неразрешимых задач на построение с помощью циркуля и линейки.

Существует много интересных задач и головоломок связанных с числом π.

Например, такая задачка: требуется с помощью не более 4-х чисел π и знаков математических действий и функций написать такие выражения, значения которых были бы от 0 до 100. Причём надо стараться, чтобы запись выражения была как можно короче (содержала меньше всего знаков), проще и красивее. Т.к. число π иррациональное, то практически везде придётся использовать округление (математическое […], в большую `|~...~| ` или меньшую `floor(...) ` сторону). Также можно использовать не совсем корректные обозначения, но тем не менее, довольно часто используемые, например расширение гамма-функции на факториал: `π! = Gamma(π+1) `. С факториалом красивее :)

Я придумал вот такие выражения, а вы сможете их улучшить?

• `0 = π-π `
• `1 = π:π `
• `2 = (π+π):π `
• `3 = [π] = (π+π+π):π `
• `4 = |~π~| `
• `5 = |~π!-π~| `
• `6 = [π+π] `
• `7 = [π!] = |~π+π~| `
• `8 = |~π!~| `
• `9 = [π]*[π] `
• `10 = [π*π] `
• `11 = floor(π^π:π) `
• `12 = [π^π:π] `
• `13 = [π*π+π] `
• `14 = |~π+π~|+|~π+π~| `
• `15 = |~π!-π~|*[π] `
• `16 = [π*π]+[π+π] `
• `17 = [π*π]+|~π+π~| `
• `18 = [π]*[π]+[π]*[π] `
• `19 = floor((π+π)*π) `
• `20 = [(π+π)*π] `
• `21 = [π!]*[π] `
• `22 = [[π!]*π] `
• `23 = [π*π!] `
• `24 = [π!]*[π]+[π] `
• `25 = |~π!-π~|*|~π!-π~| `
• `26 = [π*π!]+[π] `
• `27 = [π]*[π]*[π] `
• `28 = [π*[π]*[π]] `
• `29 = [π]*floor(π*π) `
• `30 = [π*π]*[π] `
• `31 = [π*π*π] `
• `32 = [[π]^π] `
• `33 = floor(π^π:π)*[π] `
• `34 = [π*π*π]+[π] `
• `35 = [π^π:π]*[π] `
• `36 = [π^π] `
• `37 = floor([π^π]+sqrt(π)) `
• `38 = [π^π+sqrt(π)] `
• `39 = [π^π]+[π] `
• `40 = [π^π+π] `
• `41 = [π^π]+|~π!-π~| `
• `42 = [π!]*[π]+[π!]*[π] `
• `43 = [π!]*[π]+[[π!]*π] `
• `44 = [[π!]*π]+[[π!]*π] `
• `45 = [[π!]*π]+[π*π!] `
• `46 = [π*π!]+[π*π!] `
• `47 = [π!]*|~π!~|-[π]*[π] `
• `48 = [π!]*|~π!~|-|~π!~| `
• `49 = [π!]*|~π!~|-[π!] `
• `50 = [π!]*|~π!~|-[π+π] `
• `51 = [π!]*|~π!~|-|~π!-π~| `
• `52 = [π!]*|~π!~|-|~π~| `
• `53 = [[π]^π]+[π!]*[π] `
• `54 = [[π]^π]+[[π!]*π] `
• `55 = [[π]^π]+[π*π!] `
• `56 = [π!]*|~π!~| `
• `57 = [π^π]+[π!]*[π] `
• `58 = [π^π]+[[π!]*π] `
• `59 = [π^π]+[π*π!] `
• `60 = [π*π]*[π]*[sqrt(π)] `
• `61 = [π^π*sqrt(π)-π] `
• `62 = [π^π*sqrt(π)]-[π] `
• `63 = floor([π^π]*sqrt(π)) `
• `64 = [[π^π]*sqrt(π)] `
• `65 = [π^π*sqrt(π)] `
• `66 = floor([π^π]*sqrt(π)+π) `
• `67 = [[π^π]*sqrt(π)+π] `
• `68 = [π^π*sqrt(π)]+[π] `
• `69 = [π*π!]*[π] `
• `70 = floor([π^π+π]*sqrt(π)) `
• `71 = [[π^π+π]*sqrt(π)] `
• `72 = [π^π]+[π^π] `
• `73 = [π^π+π^π] `
• `74 = [[π^π*sqrt(π)]*ln(π)] `
• `75 = [([π!]*[π]+[π])*π] `
• `76 = |~([π!]*[π]+[π])*π~| `
• `77 = floor(|~π~|^π) `
• `78 = [|~π~|^π] `
• `79 = [(π^π+π)*[sqrt(π)]] `
• `80 = [π^π+π]*[sqrt(π)] `
• `81 = [π]*[π]*[π]*[π] `
• `82 = [|~π~|^π]+|~π~| `
• `83 = [floor(|~π~|^π)+π+π] `
• `84 = [[|~π~|^π]+π+π] `
• `85 = [|~π~|^π]+|~π~|+[π] `
• `86 = [|~π~|^π]+|~π~|+|~π~| `
• `87 = [|~π~|^π]+[π]*[π] `
• `88 = [|~π~|^π]+[π*π] `
• `89 = [[π]^π]*[π]-[π!] `
• `90 = [π]*[π*π]*[π] `
• `91 = [π]^(|~π~|)+[π*π] `
• `92 = floor([[π]^π]*[π]-π) `
• `93 = [π*π*π]*[π] `
• `94 = [[π]^π]*[π]-[sqrt(π)] `
• `95 = [[π]^π]*[π]-[ln(π)] `
• `96 = [[π]^π]*[π] `
• `97 = [π*π*π*π] `
• `98 = [[π]^π]*[π]+|~sqrt(π)~| `
• `99 = [[π]^π]*[π]+[π] `
• `100 = [π*π]*[π*π] `

Кстати, если разрешить в этой задачке не только математические правила и функции, но и «программерские» фишечки типа конкатенации, битовых сдвигов, логических операндов и т.п., то можно делать, например, такие варианты (в зависимости от используемого синтаксиса языка программирования):

33 = [π]||[π] = [π]&[π] = [π].[π] (конкатенация)
43 = [[π!]^[π]>>[π]] (сдвиговые операции)

В рамках этой же задачки можно попробовать придумать выражение, которое даст самое большое целочисленное значение. Например,

• `[π^(π^(π^π))] = ` 2 598 761 979 625 198

хотя можно записать и такое:

• `[(|~π!~|)^((|~π!~|)^((|~π!~|)^(|~π!~|)))] = 8^(8^(8^8)) ~= ` 2,41·10⁴⁶²

Но и это не самое большое Если почитать «занимательную гугологию» по ссылкам ниже, то можно понять, что число выше - это лишь цветочки…

А можно наоборот - попытаться найти самое маленькое по модулю, но не равное нулю.

В общем, развлекухи не на один день.

Люди знакомы с числом Пи очень долго, и на протяжении всего времени знакомства пытаются понять и изучить это число. Хороший способ изучения чего-либо цифрового – попробовать представить изучаемый объект в более-менее аналоговом или графическом виде. Результаты таких «исследований» можно посмотреть ниже.

Если нарисовать окружность, разделить её на 10 секторов по количеству десятичных цифр и затем каждую пару цифр числа Пи соединять друг с другом разноцветной дугой между соответствующими секторами с небольшим сдвигом, то получается вот такая красивая визуализация:

А тут каждая последующая цифра записывается в сектор предыдущей цифры.

Здесь размер цифры показывает, насколько она арифметически близка к соседним цифрам.

А на этой картинке цифры числа π в количестве 351 штуки записаны символами из 54 разных языков. Красным цветом выделены цифры в порядке 345678901234567890….

Такие визуализации можно использовать как для изучения свойств числа, так и просто, как говорится, «для балдежа». Например, сделать себе красивый принт на футболке.

Есть много сайтов, посвящённым таким визуализациям. Один из них - http://mkweb.bcgsc.ca/pi/art/.

• Занимательная Гугология:

• http://lihachevss.ru/zg_ch1.html – Часть I Числа
• http://lihachevss.ru/zg_ch2.html – Часть II Бесконечность
• http://lihachevss.ru/zg_ch3.html – Часть III Рекурсии на бесконечных рекурсиях
• http://lihachevss.ru/zg_ch4.html – Часть IV Рекурсии на несчетных рекурсиях
• http://lihachevss.ru/zg_ch5.html – Часть V Рекурсии на недостижимых рекурсиях
• http://lihachevss.ru/zg_ch6.html – Часть VI Рекурсии на стационарных рекурсиях

• https://scorcher-7.livejournal.com/691.html – часть 1. Как записывать большие числа?
• https://scorcher-7.livejournal.com/1022.html – часть 2. Есть ли что-нибудь за пределами бесконечности?
• https://scorcher-7.livejournal.com/1165.html – часть 3. Как упорядочить бесконечность?
• https://scorcher-7.livejournal.com/1283.html – часть 4. Какое число самое большое? (1)
• https://scorcher-7.livejournal.com/1675.html – часть 5. Какое число самое большое? (2)
• https://scorcher-7.livejournal.com/1818.html – часть 6. Можно ли вычислить невычислимое?
• https://scorcher-7.livejournal.com/2151.html – постскриптум

• https://new-science.ru/15-interesnyh-faktov-o-chisle-pi-o-kotoryh-vy-vozmozhno-ne-znali/
• http://light-science.ru/o/krasivaya-vizualizatsiya-chisla.html

• http://mkweb.bcgsc.ca/pi/art/ – сайт, посвящённый визуализациям числа Пи