2019

Сведения о числе 2019

Число 2019 является:

рациональным
четырёхзначным
составным (не простым), так как помимо делителей 1 и 2019 имеет ещё два делителя - 3 и 673.
полупростым числом, так как все делители - простые числа.

Математика и 2019

2+0+1+9 = 12
нумерологический корень [2019] = 2+0+1+9 = 12 = 1+2 = 3
всего 4 делителя: 1, 3, 673 и 2019; сумма делителей $1+3+673+2019=2696$
$2019=3*673$
произведение всех цифр: $2*0*1*9=0$
2019 и 0,00049529470034670629024269440316989.. являются взаимно обратными числами, то есть их произведение = 1

$\sin 2019°~~-0,6293$
$\cos 2019°~~-0,7771$
$\tg 2019°~~0,8098$

$\sin 2019~~0,8645$
$\cos 2019~~-0,5027$
$\tg 2019~~-1,7196$

$\ln 2019~~7,6104$
$\lg 2019~~3,3051$

2019₁₀ = 11111100011₂
2019₁₀ = 2202210₃
2019₁₀ = 3743₈
2019₁₀ = 7E3₁₆
2019₁₀ = 5B5₁₉
2019₁₀ = 1V3₃₂

$2019^2 = 4076361$
$2019^3 = 8230172859$
$\sqrt2019 ~~ 44,933283877321942292823446392152$
$\root(20)(19) ~~ 1,1586110870184631536731716537409$
$2019° ~~ 35,238197597765514158089316615785$ радиан
$2019$ радиан $~~ 115680,17883691320585025547456968°$

две тысячи девятнадцать → 3 6 12 букв
2019 = MMXIX
В виде кода азбуки Морзе: ..— —– .—- —-.

2019 байтов = 1 килобайт 995 байтов
MD-5(2019) = ea6b2efbdd4255a9f1b3bbc6399b58f4
CRC32(2019) = 3327493404
SHA1(2019) = 0c422ba64421103f8f58fc3c8676caf9c7c73178
SHA256(2019) = 023e33504ab909cf87a6f4e4e545090e40bdc0a2153e5b68b19f7fad2b737904
Base64(2019) = MjAxOQ==
C++ 2019 = 0x0007E3, 0x7E3
Pascal 2019 = $0007E3
UTC(2019) = UTC(+3) Москва, Россия четверг, 1 января 1970 г., 3:33:39 Москва, стандартное время
2019 → IPv4 = 0.0.7.227
RGB(2019) = #0007E3 - (0, 7, 227)

20°19'

20/9 = 2,(2)
20\9 = 2
2⋅19 = 38
20⋅19 = 380
201/9 = 22,(3)

2019₁₆ = 0x2019 = 8217₁₀
20¹⁹ = 5242880000000000000000000 = 5,24288·10²⁴
201⁹ = 535506216522273441801
20₁₉ = 38₁₀
201₉ = 163₁₀

20¹·9 = 180
20!/19! = 20
20/19 = 1,(052631578947368421)

$C_20^19$ = 20
$A_20^19$ = 2432902008176640000
$2019 = 3+sum_(n=1)^63 n$

Задача

20:19

«Чему равен угол между часовой и минутной стрелкой, когда на часах 20:19:00?»
Минутная стрелка за одну минуту проходит 6°, а за 19 прошла 6°·19=114°. Часовая стрелка за 1 час поворачивается на 30°. Считаем, что стрелки движутся плавно, а не скачками. За 8 полных часов часовая прошла 30°·8=240°, плюс за 19 минут довернулась на 19/60 от 30°, то есть на 9,5°. Итого, часовая прошла 240°+9,5°=249,5°. Угол между часовой и минутной стрелками = 249,5°-114° = 135,5°.

Календарь на 2019 год

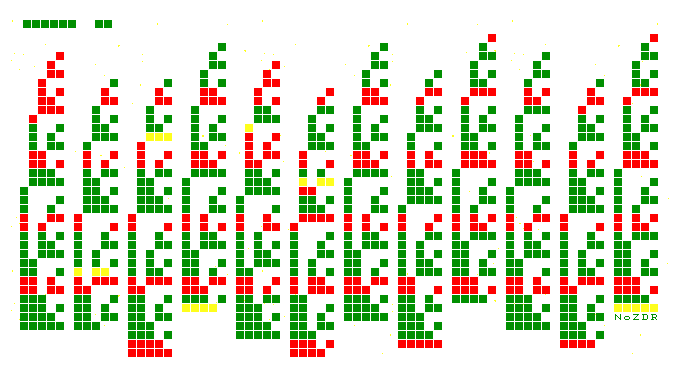
Это бинарный производственный календарь на 2019 год. 12 «ёлочек» с веточками-днями в двоичном виде раскрашены в три цвета: рабочие дни - зелёным, предпраздничные - жёлтым, нерабочие - красным. О том, как сделан этот календарь, можно почитать на странице Производственный календарь.

2019 из последовательных цифр

$2019 = (1111-111+11-1)*(1+1)-1$
$2019 = 2222-222+22-2-2:2$
$2019 = [\sqrt3333333]+[\sqrt33333]+33:3+3:3$
$2019 = [44^4:444:4-44-44-4]+4:4$
$2019 = |__5,5^5-55*55+55:5__|+5:5$
$2019 = [(6,6^6+6^6):66+66-6]$
$2019 = |__\sqrt7777777-777+7__|+7:7$
$2019 = [\sqrt8888888]-888-8*8-8-[\ln8]$
$2019 = 999+999+9+9+\sqrt9$
$2019 = (0!+0!+0!+0!)^{0!+0!+0!+0!+0!+0!}/{0!+0!}-(0!+0!+0!+0!)^{0!+0!+0!}/{0!+0!}+0!+0!+0!$

Последовательные числа из 2019

$0 = 2*0^19$
$1 = 20-19$
$2 = [2,019]$
$3 = 201\\9$
$4 = 2+0-1+\sqrt9$
$5 = (2+0)*1+\sqrt9$
$6 = -2-0-1+9$
$7 = -2-0*1+9$
$8 = -2^0*1+9$
$9 = 2^0*1*9$
$10 = 20-1-9$
$11 = 20^1-9$
$12 = 20+1-9$
$13 = 2+0!+1+9$
$14 = [\sqrt201]+floor(\sin9)$
$15 = floor(20:\lg19)$
$16 = 20-1-\sqrt9$
$17 = 20*1-\sqrt9$
$18 = 20-[1,9] = (2^0+1)*9$
$19 = 20-1^9 = 2^0*19$
$20 = [20,19] = 20*1^9 = 20!:19!$
$21 = 20+1^9$
$22 = [201:9]$
$23 = 20*1+\sqrt9$
$24 = 20+1+\sqrt9$
$25 = [\lg20*19]$
$26 = [20*\lg19]$
$27 = (2+0+1)*9$
$28 = 20-1+9$
$29 = 20⋅1+9$
$30 = 20+1+9$
$31 = [20:\ln1,9]$
$32 = |~20:\ln1,9~|$
$33 = |~(e^2+0)*\sqrt19~|$
$34 = |__\sqrte*20+1,9__|$
$35 = [\sqrte*20+1,9]$
$36 = (2+0!+1)*9$
$37 = [e*\sqrt201-\sqrt\sqrt9]$
$38 = 20*1,9$
$39 = 20+19$
$40 = [20*1,(9)]$
$41 = [e^π+20-[1,9]]$
$42 = |__sqrt{201*9}__|$
$43 = [sqrt{201*9]$
$44 = |__\sqrt2019__|$
$45 = ([\sqrt20]+1)*9$
$46 = [20^{\lg19}]$
$47 = |__\ln201*9__|$
$48 = [\ln201*9]$
$49 = [(\sqrt20+1)*9]$
$50 = |~(\sqrt20+1)*9~|$

−Навигация