• Онлайн: 2
Игра NBIN
Давно хотелось написать какую-нибудь простенькую игрушку, в которую было бы можно играть на компьютере и на телефоне, чтобы была более-менее логическая, динамичная, с программистским уклоном и при этом отвечала концепции ММЦК. И вот, осмысливая в очередной раз эту концепцию, в процессе написания сказки про ёлочки мне пришла в голову идея сделать игрушку на базе двоичного (бинарного) кода.
Далее, если в теме, что это такое, то можно смело пропустить.
Итак, игрушка должна быть про бинарный код и чтобы работала и на компьютере и на телефоне одновременно. Проще, чем реализовать это на html+javascript и разместить у себя на сайте, в голову не пришло. Решил ограничиться чистым фронтэндом. Может быть, потом придумаю какой-нибудь бэкэнд с сохранялками, стеной плачаславы и пр. А может быть и не надо этого. А пока вот, что получилось. NBIN = NoZDR's Binary.
Жмите вот эту ссылку, игра откроется в новом окне:
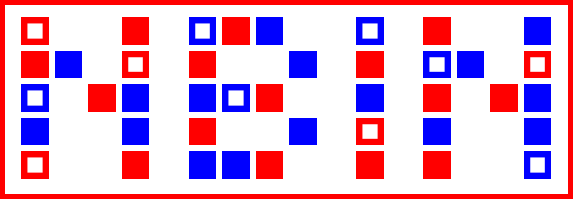
А вот как игра выглядит:
Игра NBIN несложная, её можно пройти, сделав минимум 502 шага. На это у меня уходит чуть более пяти минут. Но обычно шагов я делаю больше. Потому что следовать идеальной стратегии, когда на каждом шагу открываешь новый вариант, довольно сложно. Если хочется узнать побольше про оптимальную стратегию с минимальным количеством шагов, почитайте про Код_Грея.